
如图,在平面直角坐标系中,△ABC和△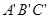 是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
(1)请你根据位似的特征并结合点B的坐标变化回答下列问题: ①若点A(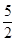 ,3),则A′的坐标为 ;②△ABC与△
,3),则A′的坐标为 ;②△ABC与△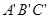 的相似比为 ;
的相似比为 ;
(2)若△ABC的面积为m,求△A′B′C′的面积.(用含m的代数式表示)
科目:初中数学 来源: 题型:解答题
如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E、F、G运动的时间为t(单位:s).
(1)当t= s时,四边形EBFB′为正方形;
(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;
(3)是否存在实数t,使得点B′与点O重合?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.
(1)若BD是AC边上的中线,如图1,求 的值;
的值;
(2)若BD是∠ABC的角平分线,如图2,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
老师要求同学们在图①中 内找一点P,使点P到OM、ON的距离相等.
内找一点P,使点P到OM、ON的距离相等.
小明是这样做的:在OM、ON上分别截取OA=OB,连结AB,取AB中点P,点P即为所求.
请你在图②中的 内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.
内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出 的值.
的值.

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD中,AD=3厘米,AB=a厘米(a>3).动点M,N同时从B点出发,分别沿B?A,B?C运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于P,Q.当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.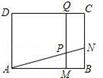
(1)若a=4厘米,t=1秒,则PM= _________ 厘米;
(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围;
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形PMBN,梯形PQDA,梯形PQCN的面积都相等?若存在,求a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读下面的材料:
小明遇到一个问题:如图(1),在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G. 如果 ,求
,求 的值.
的值. 
他的做法是:过点E作EH∥AB交BG于点H,则可以得到△BAF∽△HEF.
请你回答:(1)AB和EH的数量关系为 ,CG和EH的数量关系为 , 的值为 .
的值为 .
(2)如图(2),在原题的其他条件不变的情况下,如果 ,那么
,那么 的值为 (用含a的代数式表示).
的值为 (用含a的代数式表示).
(3)请你参考小明的方法继续探究:如图(3),在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果 ,那么
,那么 的值为 (用含m,n的代数式表示).
的值为 (用含m,n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上一点(不与点A、B重合),连结CO并延长CO交⊙O于点D,连结AD.
(1)求弦长AB的长度;(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com