
 ФЛ¶ЇµДК±јдОЄtГлЈЁ0ЎЬtЎЬ4Ј©Ј®
ФЛ¶ЇµДК±јдОЄtГлЈЁ0ЎЬtЎЬ4Ј©Ј®| 3 |
| 2 |
| 5 |
| 2 |
| 15 |
| 8 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| PB2-QB2 |
| (5-t)2-(4-t)2 |
| 9-2t |
| PM2+OM2 |
(
|
t2-
|
| OP2-PQ2 |
t2-
|
t2-
|
| NQ |
| PQ |
| PQ |
| OQ |
| ||
| PQ |
| PQ |
| t |
| 1 |
| 5 |
| 18 |
| 5 |
| 18 |
| 5 |
| 1 |
| 5 |
| 18 |
| 5 |
t2-
|
(
|
| 18 |
| 5 |
| 15 |
| 25 |
| 24 |
| 5 |
| 8 |
| 5 |
-15ЎА20
| ||
| 13 |
20
| ||
| 13 |
| 8 |
| 5 |
20
| ||
| 13 |


 ГыМвСµБ·ПµБРґр°ё
ГыМвСµБ·ПµБРґр°ё ЖЪД©јЇЅбєЕПµБРґр°ё
ЖЪД©јЇЅбєЕПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
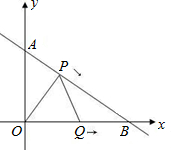
 ЈЁ2013•ДПНЁТ»ДЈЈ©ТСЦЄЈєИзНјЈ¬Ц±y=2x+bЅ»xЦбУЪµгBЈ¬Ѕ»yЦбУЪµгCЈ¬µгAОЄxЦбХэ°лЦбЙПТ»µгЈ¬AO=COЈ¬ЎчABCµДГж»эОЄ12Ј®
ЈЁ2013•ДПНЁТ»ДЈЈ©ТСЦЄЈєИзНјЈ¬Ц±y=2x+bЅ»xЦбУЪµгBЈ¬Ѕ»yЦбУЪµгCЈ¬µгAОЄxЦбХэ°лЦбЙПТ»µгЈ¬AO=COЈ¬ЎчABCµДГж»эОЄ12Ј®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
 ИзНјЈ¬ТСЦЄBЈЁ0Ј¬4Ј©Ј¬µгAФЪµЪТ»ПуПЮЈ¬ЗТABЎНyЦбЈ¬ЎПA=30ЎгЈ®
ИзНјЈ¬ТСЦЄBЈЁ0Ј¬4Ј©Ј¬µгAФЪµЪТ»ПуПЮЈ¬ЗТABЎНyЦбЈ¬ЎПA=30ЎгЈ®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈєµҐїЖНхЕЖЎЎЎЎѕЕДкј¶КэС§(ЙП) МвРНЈє044
ТСЦЄµИСьЦ±ЅЗИэЅЗРОABCµДµЧ±ЯОЄABЈ¬Ц±ПЯl№эЦ±ЅЗ¶ҐµгCЈ¬·Ц±р№эµгAЎўBЧчlµДґ№ПЯЈ¬ґ№Чг·Ц±рОЄEЎўFЈ®
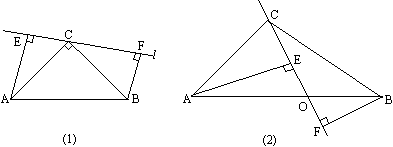
(1)ИзНј(1)Ј¬µ±lУлABІ»ПаЅ»К±Ј¬ЗуЦ¤ЈєEFЈЅAEЈ«BF
(2)ИзНј(2)Ј¬µ±lУлABПаЅ»УЪOЈ¬ЗТAOЈѕBOЈ¬ЖдЛыМхјюІ»±дЈ¬ЗлІВПлEFЎўAEЎўBFјдµДµИБї№ШПµЈ¬ІўЦ¤ГчЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє044
ИзНјЈ¬ТСЦЄµИСьЦ±ЅЗИэЅЗРОABCµДµЧ±ЯОЄABЈ¬Ц±ПЯl№эЦ±ЅЗ¶ҐµгCЈ¬№эµгAЈ¬B·Ц±рЧчlµДґ№ПЯAEЈ¬EFЈ®
ИфЦ±ПЯlІ»УлµЧ±ЯABПаЅ»Ј¬ИзНјўЩЈ¬ФтУРEF=AEЈ«BFЈ¬ИфЦ±ПЯlУлµЧ±ЯABПаЅ»УЪµгO(AOЈѕBO)Ј¬ИзНјўЪЈ¬ФтЙПКцЅбВЫ»№іЙБўВрЈїИфІ»іЙБўЈ¬ЗлЦ±ЅУРґіцЛьГЗµДµИБї№ШПµКЅЈ»ИфіЙБўЈ¬ЗлЛµГчАнУЙЈ®
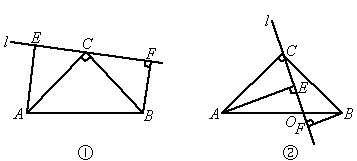
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com