
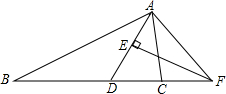
 如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由.
如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由. 科目:初中数学 来源: 题型:选择题
| A. | (0,4) | B. | (-3,1) | C. | (0,-2) | D. | (3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
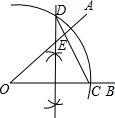 如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.
如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我市百岁以上老人的健康情况 | B. | 调查某电视连续剧在全国的收视率 | ||
| C. | 了解一批炮弹的杀伤半径 | D. | 了解一批袋装食品是否含有防腐剂 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com