

分析 (1)连接BD,交EF于点O,利用已知条件和折叠的性质证明BE=BF和EF与BD垂直平分,即可证明四边形DFBE是菱形;
(2)根据平行四边形的各种判定方法即可直接写出图2中的所有平行四边形.
解答 证明:(1)连接BD,交EF于点O,
∵AB=BC,点D是AC的中点,
∴BD⊥AC,∠ABD=∠DBC,
由折叠可知EF⊥BD,OB=OD,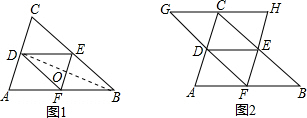
∴BE=BF,
∴OE=OF,
∴EF与BD垂直平分,
∴四边形DFBE是菱形;
(2)如图2中共有五个平行四边形(不包括以BF为一边的平行四边形).
分别是□ADEF;□ACHF;□DCHE;□DGCE;□DCEF.
点评 本题考查了菱形的判定和性质、平行四边形的判定和性质以及折叠的性质,题目的综合性较强,具有一定的开放性,解题的关键是熟记菱形、平行四边形的各种判定方法以及其各种性质.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 32•33=65 | B. | (2×102)(3×103)=6×106 | ||
| C. | (-xy)2•(xy)3=x5y5 | D. | (a4b)2=a4b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
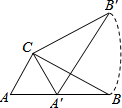 三角板∠ACB=90°,∠B=30°,BC=6,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边起始位置即停止转动,则B点转过的路径BB′的长为2π.
三角板∠ACB=90°,∠B=30°,BC=6,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边起始位置即停止转动,则B点转过的路径BB′的长为2π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.9×103 | B. | 3.9×108 | C. | 39×108 | D. | 3.9×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
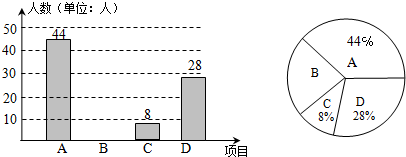
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
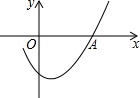 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )| A. | b2<4ac | B. | ac>0 | C. | 2a-b=0 | D. | a-b+c=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com