
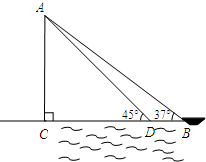
 (2012•栖霞区一模)如图,在距离水面高为6m的岸上A处用绳子拉船靠岸,当小船被拉到B处时绳子与水面的夹角为37°,又收绳4s后,船被拉至点D处,此时绳子与水面的夹角为45°.
(2012•栖霞区一模)如图,在距离水面高为6m的岸上A处用绳子拉船靠岸,当小船被拉到B处时绳子与水面的夹角为37°,又收绳4s后,船被拉至点D处,此时绳子与水面的夹角为45°.| 2 |
| AC |
| BC |
| 6 |
| BC |
| 6 |
| 0.75 |
| AC2+BC2 |
| AC2+CD2 |
| 2 |
| 10-8.4 |
| 4 |


科目:初中数学 来源: 题型:
 (2012•栖霞区一模)如图,已知在△OBC中,∠BOC=90°,且OB=OC,△OAB是正三角形,将△OAB绕点O按逆时针方向旋转得到△OCD,旋转角为a(0°<a<180°),则∠a=
(2012•栖霞区一模)如图,已知在△OBC中,∠BOC=90°,且OB=OC,△OAB是正三角形,将△OAB绕点O按逆时针方向旋转得到△OCD,旋转角为a(0°<a<180°),则∠a=查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•栖霞区一模)如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BE⊥CD,垂足为E,AD=2,CD=4
(2012•栖霞区一模)如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BE⊥CD,垂足为E,AD=2,CD=4| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•栖霞区一模)如图,一次函数y=kx+b的图象与反比例函数 y=
(2012•栖霞区一模)如图,一次函数y=kx+b的图象与反比例函数 y=| m |
| x |
| m |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com