
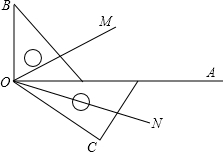
 如图,两块三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC.
如图,两块三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC. ∠BOC=
∠BOC= ×120°=60°,
×120°=60°, ∠AOC=
∠AOC= ×30°=15°,
×30°=15°, ∠BOC=
∠BOC= ×110°=55°,
×110°=55°, ∠AOC=
∠AOC= ×20°=10°,
×20°=10°, ∠BOC=
∠BOC= ×(90°+α),
×(90°+α), ∠AOC=
∠AOC= α,
α, ×(90°+α)-
×(90°+α)- α=45°+
α=45°+ α-
α- α=45°;
α=45°; ∠BOC=
∠BOC= (β+30°),
(β+30°), ∠AOC=
∠AOC= ×30°=15°,
×30°=15°, (β+30°)-15°=
(β+30°)-15°= β+15°-15°=
β+15°-15°= β.
β.

科目:初中数学 来源: 题型:
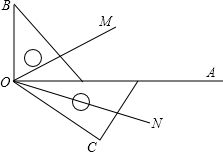 如图,两块三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC.
如图,两块三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC.查看答案和解析>>
科目:初中数学 来源: 题型:
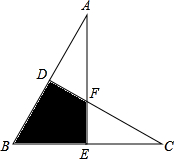 将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.
将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.
将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.查看答案和解析>>
科目:初中数学 来源:2009-2010学年辽宁省大连市志成学校七年级(下)入学考试数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com