∑÷Œˆ£∫£®1£©«Û≥ˆ∑Ω≥Ãax
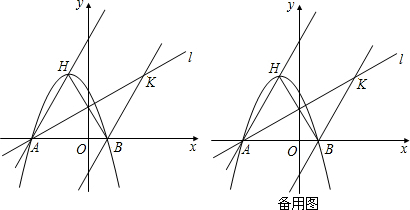
2+2ax-3a=0£®a°Ÿ0£©£¨º¥ø…µ√µΩAµ„◊¯±Í∫ÕBµ„◊¯±Í£ª∞—Aµƒ◊¯±Í¥˙»Î÷±œþlº¥ø…≈–∂œA «∑Ò‘⁄÷±œþ…œ£ª
£®2£©∏˘æðµ„H°¢Bπÿ”⁄π˝Aµ„µƒ÷±œþl£∫y=
x+
∂‘≥∆£¨µ√≥ˆAH=AB=4£¨π˝∂•µ„H◊˜HC°ÕABΩªAB”⁄Cµ„£¨«Û≥ˆAC∫ÕHCµƒ≥§£¨µ√≥ˆ∂•µ„Hµƒ◊¯±Í£¨¥˙»Î∂˛¥Œ∫Ø ˝Ω‚Œˆ Ω£¨«Û≥ˆa£¨º¥ø…µ√µΩ∂˛¥Œ∫Ø ˝Ω‚Œˆ Ω£ª
£®3£© ◊œ»≈–∂®°˜ABH «µ»±þ»˝Ω«–Œ£¨Ω¯∂¯ππ‘Ï÷±Ω«»˝Ω«–Œµ√≥ˆtµƒ÷µº¥ø…£ª
£®4£©µ√≥ˆ÷±œþAH£¨BKµƒΩ‚Œˆ Ω£¨µ√µΩ∑Ω≥Ã◊È
£¨º¥ø…«Û≥ˆKµƒ◊¯±Í£¨∏˘æðµ„H°¢Bπÿ”⁄÷±œþAK∂‘≥∆£¨µ√≥ˆHN+MNµƒ◊Ó–°÷µ «MB£¨π˝µ„K◊˜÷±œþAHµƒ∂‘≥∆µ„Q£¨¡¨Ω”QK£¨Ωª÷±œþAH”⁄E£¨µ√µΩBM+MKµƒ◊Ó–°÷µ «BQ£¨º¥BQµƒ≥§ «HN+NM+MKµƒ◊Ó–°÷µ£¨”…π¥π…∂®¿Ìµ√QB=8£¨º¥ø…µ√≥ˆ¥∞∏£Æ
Ω‚¥£∫Ω‚£∫£®1£©“¿Ã‚“‚£¨µ√ax
2+2ax-3a=0£®a°Ÿ0£©£¨
º¥x
2+2x-3=0£¨
Ω‚µ√x
1=-3£¨x
2=1£¨
°þBµ„‘⁄Aµ„”“≤ý£¨
°ýAµ„◊¯±ÍŒ™£®-3£¨0£©£¨Bµ„◊¯±ÍŒ™£®1£¨0£©£¨
¥£∫A°¢B¡Ωµ„◊¯±Í∑÷± «£®-3£¨0£©£¨£®1£¨0£©£Æ
°þ÷±œþl£∫y=
x+
£¨
µ±x=-3 ±£¨y=
°¡£®-3£©+
=0£¨

°ýµ„A‘⁄÷±œþl…œ£Æ
£®2£©°þµ„H°¢Bπÿ”⁄π˝Aµ„µƒ÷±œþl£∫y=
x+
∂‘≥∆£¨
°ýAH=AB=4£¨
»ÁÕº1£¨π˝∂•µ„H◊˜HC°ÕABΩªAB”⁄Cµ„£¨
‘ÚAC=
AB=2£¨HC=2
£¨
°ý∂•µ„H£®-1£¨2
£©£¨
¥˙»Î∂˛¥Œ∫Ø ˝Ω‚Œˆ Ω£¨Ω‚µ√a=-
£¨
°ý∂˛¥Œ∫Ø ˝Ω‚Œˆ ΩŒ™y=-
x
2-
x+
£¨
¥£∫∂˛¥Œ∫Ø ˝Ω‚Œˆ ΩŒ™y=-
x
2-
x+
£¨
£®3£©°þAµ„◊¯±ÍŒ™£®-3£¨0£©£¨µ„H£®-1£¨2
£©£¨
°ýAH=
=4£¨
°þBµ„◊¯±ÍŒ™£®1£¨0£©£¨µ„H£®-1£¨2
£©£¨
°ýBH=
=4£¨
°þAµ„◊¯±ÍŒ™£®-3£¨0£©£¨Bµ„◊¯±ÍŒ™£®1£¨0£©£¨
°ýAB=4£¨º¥AB=AH=BH=4£¨
°ý°˜ABH «µ»±þ»˝Ω«–Œ£¨
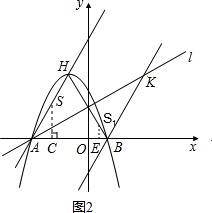
»ÁÕº2£¨π˝µ„S◊˜SC°ÕAB”⁄µ„C£¨π˝µ„S
1◊˜S
1E°ÕAB”⁄µ„E£¨
…˵±t√Î ±£¨“‘µ„sŒ™‘≤–ƒµƒ‘≤”ΡΩ◊¯±Í÷·∂ºœý«–£Æ
‘ÚAS=t£¨AC=
t£¨SC=
t£¨
¥À ±SC=CO£¨
º¥
t=3-
t£¨
Ω‚µ√£∫t=3£®
-1£©£¨
Õ¨¿Ìø…µ√£∫S
1B=AH+HB-t=8-t£¨BE=
£¨S
1E=
£¨
µ±EO=S
1E£¨
º¥1-
=
£¨
Ω‚µ√£∫t=9-
£¨
π µ±t=3£®
-1£©ªÚt=9-
±£¨“‘µ„sŒ™‘≤–ƒµƒ‘≤”ΡΩ◊¯±Í÷·∂ºœý«–£Æ
£®4£©°þAµ„◊¯±ÍŒ™£®-3£¨0£©£¨µ„H£®-1£¨2
£©£¨
°ýΩ´¡Ωµ„¥˙»ÎΩ‚Œˆ Ωy=kx+b£¨
µ√≥ˆ
£¨
Ω‚µ√£∫
£¨
π ÷±œþAHµƒΩ‚Œˆ ΩŒ™y=
x+3
£¨
°þ÷±œþBK°ŒAHΩª÷±œþl”⁄Kµ„£¨
°ý÷±œþBKµƒΩ‚Œˆ ΩŒ™£∫y=
x+b£¨
Ω´Bµ„◊¯±Í¥˙»Î«Û≥ˆ£¨
÷±œþBKµƒΩ‚Œˆ ΩŒ™£∫y=
x-
£¨
”…
£¨
Ω‚µ√
£¨
º¥K£®3£¨2
£©£¨
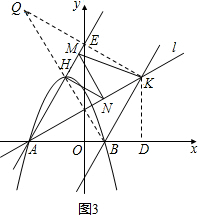
‘ÚBK=4£¨
°þµ„H°¢Bπÿ”⁄÷±œþAK∂‘≥∆£¨K£®3£¨2
£©£¨
°ýHN+MNµƒ◊Ó–°÷µ «MB£¨KD=KE=2
£¨
»ÁÕº3£¨π˝µ„K◊˜÷±œþAHµƒ∂‘≥∆µ„Q£¨¡¨Ω”QK£¨Ωª÷±œþAH”⁄E£¨KD=KE=2
£¨
‘ÚQM=MK£¨QE=EK=2
£¨AE°ÕQK£¨
°ýBM+MKµƒ◊Ó–°÷µ «BQ£¨º¥BQµƒ≥§ «HN+NM+MKµƒ◊Ó–°÷µ£¨
°þBK°ŒAH£¨
°ý°œBKQ=°œHEQ=90°„£¨
”…π¥π…∂®¿Ìµ√QB=8£¨
°ýHN+NM+MKµƒ◊Ó–°÷µŒ™8£¨
¥£∫HN+NM+MK∫Õµƒ◊Ó–°÷µ «8£Æ







 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
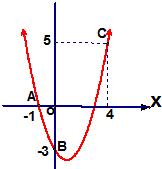 16°¢“—÷™»ÁÕº£¨∂˛¥Œ∫Ø ˝y=ax2+bx+cµƒÕºœÛπ˝A°¢B°¢C»˝µ„
16°¢“—÷™»ÁÕº£¨∂˛¥Œ∫Ø ˝y=ax2+bx+cµƒÕºœÛπ˝A°¢B°¢C»˝µ„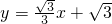 ∂‘≥∆£Æ
∂‘≥∆£Æ