解:(1)当0<t≤200,将(0,300),(200,100)代入w=at+b得
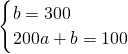
,
解得:

,
∴AB所在直线解析式为:w
1=-t+300;
当200<t≤300,
将(300,300),(200,100)代入w=ct+d得
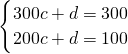
,
解得:
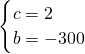
,
∴CB所在直线解析式为:w
1=2t-300;
(2)由图象可得出二次函数顶点坐标为;(150,100),代入解析式得:
w
2=k(t-150)
2+100,再将(50,150)代入得出:
150=k(50-150)
2+100,
解得:k=
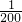
,
∴w
2=
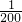
(t-150)
2+100(0<t≤300);
(3)设纯收益为y元,∵0<t≤200,则 y与 t的函数关系式:
y=-t+300-
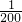
(t-150)
2-100=-
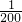
t
2+

t+
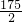
,
当 t=-

=-
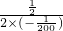
=50时,y有最大值.
分析:(1)根据图象甲,设出函数关系式,分别找出两个点的坐标,代入即可求出w与t的函数关系式;
(2)根据图象乙,利用顶点式,即可求出函数关系式;
(3)设纯收益为h,则纯收益=市场售价-种植成本,进而利用二次函数最值求法得出即可.
点评:本题考查了二次函数的应用,一次函数与分段函数,自变量取值范围在本题中都得到了体现,要根据题目给的范围,找准等量关系是解题关键.


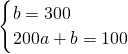 ,
, ,
,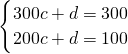 ,
,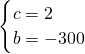 ,
,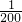 ,
,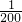 (t-150)2+100(0<t≤300);
(t-150)2+100(0<t≤300);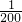 (t-150)2-100=-
(t-150)2-100=-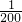 t2+
t2+ t+
t+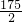 ,
, =-
=-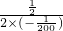 =50时,y有最大值.
=50时,y有最大值.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案