设tx-2=2x+t是关于x的方程．当方程的解分别：（1）大于0；（2）等于0；（3）小于0时，求t的取值范围．
解：方程整理为（t-2）x=2+t
当t≠2时，方程的解为：
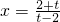
，（5分）
（1）当x＞0时，则
，
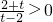
此时
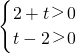
或
，
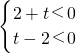
解得，t＜-2或t＞2；（10分）
（2）当x=0时，则
，
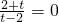
此时
，
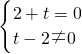
解得，t=-2；（15分）
（3）当x＜0时，则
，
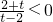
此时
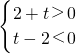
或
，
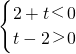
解得，-2＜t＜2．（20分）
故答案为：t＜-2或t＞2；t=-2；-2＜t＜2．
分析：先把方程化为
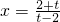
的形式，再根据x的取值范围进行解答即可．
点评：本题考查的是解一元一次方程及一元一次不等式，在解答此题方程进行变形时要注意t≠2，这是此题的易错点．
