
已知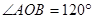 ,
,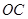 、
、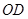 是过点
是过点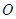 的射线,射线
的射线,射线 、
、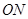 分别平分
分别平分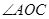 和
和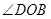 .
.
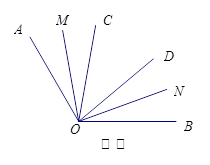
(1)如图①,若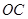 、
、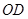 是
是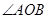 的三等分线,则
的三等分线,则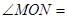 °
°
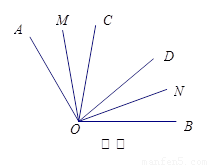
(2)如图②,若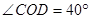 ,
,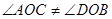 ,则
,则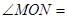 °
°
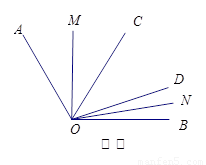
(3)如图③,在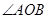 内,若
内,若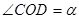 (
(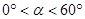 ),则
),则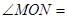 °
°

(4)将(3)中的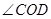 绕着点
绕着点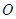 逆时针旋转到
逆时针旋转到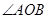 的外部(
的外部(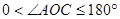 ,
,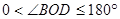 ),求此时
),求此时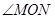 的度数.
的度数. 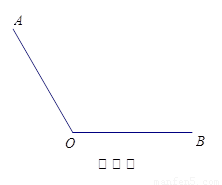
(1)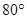 ;(2)
;(2)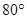 ;(3)
;(3)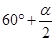 ;(4)
;(4)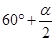 或
或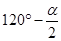
【解析】
试题分析:(1)根据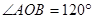 ,
,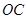 、
、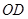 是
是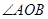 的三等分线,再结合射线
的三等分线,再结合射线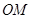 、
、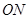 分别平分
分别平分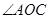 和
和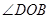 即可求得结果;
即可求得结果;
(2)由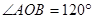 ,
, ,可得∠AOC+∠DOB的度数,再根据射线
,可得∠AOC+∠DOB的度数,再根据射线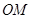 、
、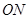 分别平分
分别平分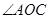 和
和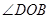 可得∠MOC+∠DON的度数,从而求得结果;
可得∠MOC+∠DON的度数,从而求得结果;
(3)由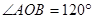 ,
,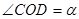 ,可表示∠AOC+∠DOB的度数,再根据射线
,可表示∠AOC+∠DOB的度数,再根据射线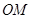 、
、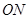 分别平分
分别平分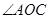 和
和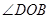 可表示∠MOC+∠DON的度数,从而得到结果;
可表示∠MOC+∠DON的度数,从而得到结果;
(4)做射线OA、OB的反向延长线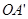 、
、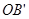 ,分五种情况:①射线OD在
,分五种情况:①射线OD在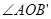 内,
内,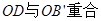 ,③
,③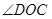 在
在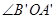 内部,④OC与
内部,④OC与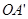 重合,⑤OC在
重合,⑤OC在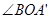 内部,根据三等分线及角平分线的性质分析即可.
内部,根据三等分线及角平分线的性质分析即可.
(1)∵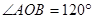 ,
,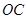 、
、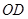 是
是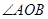 的三等分线
的三等分线
∴∠AOC=∠DOB=
∵射线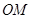 、
、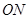 分别平分
分别平分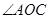 和
和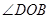
∴∠MOC=∠DON=20°
∴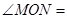 ∠MOC+∠COD+∠DON=
∠MOC+∠COD+∠DON=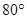 ;
;
(2)∵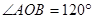 ,
,
∴∠AOC+∠DOB=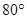
∵射线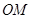 、
、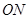 分别平分
分别平分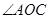 和
和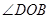
∴∠MOC+∠DON=40°
∴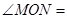 ∠MOC+∠COD+∠DON=
∠MOC+∠COD+∠DON=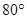 ;
;
(3)∵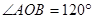 ,
,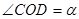
∴∠AOC+∠DOB=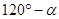
∵射线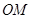 、
、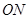 分别平分
分别平分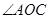 和
和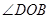
∴∠MOC+∠DON=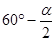
∴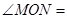 ∠MOC+∠COD+∠DON=
∠MOC+∠COD+∠DON=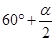 ;
;
(4)做射线OA、OB的反向延长线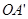 、
、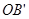
①射线OD在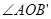 内
内
设 ,则
,则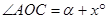
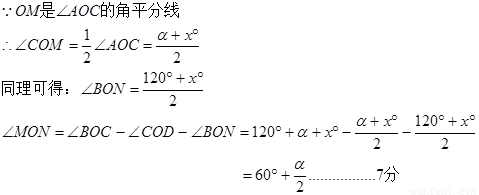
②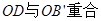
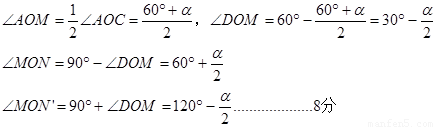
③

④OC与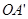 重合
重合
∠BON= ∠BOD=
∠BOD= (60º+α)="∠DON"
(60º+α)="∠DON"
∠CON=∠DON-∠DOC= (60º+α)-α=30º-
(60º+α)-α=30º- α
α
∠M′ON=90º-∠CON=90º-30º- α=60º+
α=60º+ α
α
∠MON=180º-∠M′ON=180º-(60º+ α)=120º-
α)=120º- α
α
⑤OC在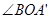 内部
内部
设∠AOD为x
∠COM= ∠AOC=
∠AOC= (α+x)
(α+x)
∠BON= ∠BOD=
∠BOD= (120º+x)
(120º+x)
∠MON=∠BOC-∠BON-∠COM=120º+x+α- (120º+x)-
(120º+x)- (α+x)=60º+
(α+x)=60º+ α
α
考点:本题考查的是角平分线的性质
点评:解答本题的关键是熟练掌握角的平分线把角分成的两个小角相等,均等于大角的一半;同时注意本题要有整体意识.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建福州文博中学七年级上学期期末考试数学试卷(带解析) 题型:解答题
已知 ,
,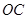 、
、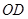 是过点
是过点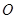 的射线,射线
的射线,射线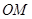 、
、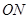 分别平分
分别平分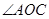 和
和 .
.
(1)如图①,若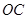 、
、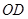 是
是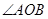 的三等分线,则
的三等分线,则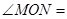 °
°
(2)如图②,若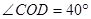 ,
,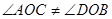 ,则
,则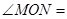 °
°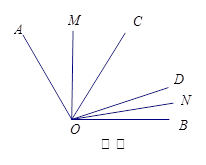
(3)如图③,在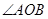 内,若
内,若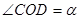 (
(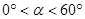 ),则
),则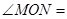 °
°
(4)将(3)中的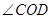 绕着点
绕着点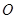 逆时针旋转到
逆时针旋转到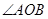 的外部(
的外部(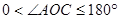 ,
,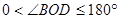 ),求此时
),求此时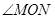 的度数.
的度数. 
查看答案和解析>>
科目:初中数学 来源:2011年湖北省武汉市青山区初二上学期数学期末考试数学卷 题型:填空题
老师布置了下列一道题:“已知∠AOB =m°,过点O做射线OC,使得∠BOC=n°(m>n),OE、OF分别为∠AOB和∠BOC的平分线,求∠EOF的度数?”小斌同学的答案是115 °,小玲同!学的答案是50°,经询问得知这两个同学的计算过程都没有出错,请你依此探究m的值为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com