练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

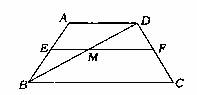
    如图，已知等腰梯形ABCD中,AD// BC. AB = CD=AD= 3,梯形中位线EF与对角线

    BU相交于点M.且BD⊥CD. 则MF的长为

    A  1.5        B 3        C3.5        D4.5


    B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    设n为正整数，且n＜＜n+1，则n的值为（   ）A、5     B、6      C、7     D、8

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；

    （2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．

    （3）运用（1）（2）解答中所积累的经验和知识，完成下题：

    如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求直角梯形ABCD的面积．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：，其中．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列手机软件图标中.既是轴对称图形又是中心对称图形的是

    查看答案和解析>>

    科目：初中数学 来源： 题型：


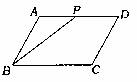
    如图，点P是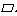ABCD边上一动点.沿A- D- C-B的路径移动，设P点经过的路径长为x,△BAP的面积是Y, 则下列能大致反映，y与x的函数关系的图象是

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    其中x为数据0,-1.-3,1.2的极差

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果一个多面体的一个面是多边形，其余各面是有一个公共顶点的三角形，那么这个多面体叫做棱锥。如图是一个四棱柱和一个六棱锥，它们各有12条棱，下列棱柱中和九棱锥的棱数相等的是

    A. 五棱柱         B. 六棱柱         C. 七棱柱         D. 八棱柱

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形” ．

    （1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，

    ∠B=80°．求∠C，∠D的度数．

      （2）在探究“等对角四边形”性质时：

          ①小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．请你证明此结论；

    ②由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等” ．你认为她的猜想正确吗？若正确，请证明；若不正确，请举出反例．

    (3)已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4．

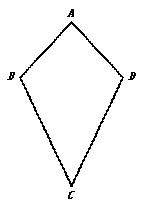    求对角线AC的长．

    第23题图1
     

    第23题图2
     
     


          

    查看答案和解析>>

    同步练习册答案