Question

在四边形ABCD中，AD∥BC，∠ABC=90°，∠ADC=135°，点P在射线BA上，连接CP，将△BCP沿着CP折叠，点B恰好落到射线AD上，若AD=2，AB=3，则BP的长为________．

Answer 1

分析：根据已知画出图形，利用垂直平分线的性质得出CQ=BC=5，CF=AB=3，进而得出QF的长，以及AQ的长，再利用翻折变换的性质以及勾股定理求出AP即可得出BP的长．
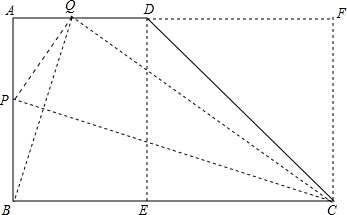
解答：解：作DE⊥BC，垂足E，延长AD，作CF⊥AD，交于F．
∵∠ADC=135°
∴∠DCE=45°
∴△DEC是等腰直角三角形
DE=CE
∵四边形ADEB是矩形
∴DE=AB=3
BE=AD=2
BC=BE+EC=5
设AD上Q点是B关于PC的对称点，
则PC是BQ的垂直平分线
∴CQ=BC=5
CF=AB=3
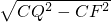
∴QF==4
DF=CE=3
∴QD=QF-DF=4-3=1，
∴AQ=AD-QD=2-1=1
设AP=x
∵PQ=PB，
∴PB=3-x
∵AP ²+AQ ²=PQ ²
∴x ²+1 ²=（3-x） ²
解得x=．
∴BP=3-=．
点评：此题主要考查了翻折变换的性质以及勾股定理和垂直平分线的性质等知识，根据已知画出正确图形是解题关键．