Question

已知?ABCD，对角线AC、BD交于点0．
（1）若AB=BC，则?ABCD是

 

；
（2）若∠BCD=90°，则?ABCD是

 

；
（3）若OA=OB，且OA⊥OB，则?ABCD是

 

；
（4）若AB=BC，且AC=BD，则?ABCD是

 

．

Answer 1

考点：平行四边形的性质

专题：

分析：（1）根据菱形的判定方法可得?ABCD是菱形；
（2）根据矩形的判定方法可得?ABCD是矩形；
（3）首先判定?ABCD是矩形，再根据菱形的判定方法可得?ABCD是菱形，因此?ABCD是正方形；
（4）根据邻边相等的平行四边形是菱形可得平行四边形ABCD是菱形，再根据对角线相等的灵性是正方形进行判定．

解答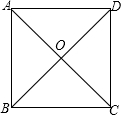：解：（1）根据邻边相等的平行四边形是菱形可得?ABCD是菱形；

（2）根据有一个角为直角的平行四边形是矩形可得?ABCD是矩形；

（3）∵四边形ABCD是平行四边形，
∴AO=CO，BO=DO，
∵OA=OB，
∴AC=BD，
∴平行四边形ABCD是矩形，
∵OA⊥OB，
∴?ABCD是正方形；

（4）∵四边形ABCD是平行四边形，AB=BC，
∴平行四边形ABCD是菱形，
∵AC=BD，
∴?ABCD是正方形．
故答案为：菱形；矩形；正方形；正方形．

点评：此题主要考查了特殊平行四边形的判定，关键是掌握菱形、矩形、正方形的判定方法．