
 如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC的角平分线,若∠AOC=70°.
如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC的角平分线,若∠AOC=70°.分析 (1)根据角的平分线的定义求得∠AOD的度数,然后根据邻补角的定义求得∠BOD的度数;
(2)首先根据∠DOE=90°,即∠COD+∠COE=90°,即可求得∠COE的度数,然后根据∠BOE=180°-∠AOD-∠DOE,求得∠BOE的度数,从而判断.
解答 解:(1)∵OD是∠AOC的角平分线(已知),∠AOC=70°
∴∠AOD=∠COD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×70°=35°(角平分线定义),
∵∠AOD+∠BOD=180°
∴∠BOD=180°-∠AOD=180°-35°=145°;
(2)答:OE平分∠BOC.
理由∵∠COE+∠COD=∠DOE,∠DOE=90°,
∴∠COE=∠DOE-∠COD=90°-35°=55°.
∵∠AOD+∠DOE+∠BOE=180°
∴∠BOE=180°-∠AOD-∠DOE=180°-35°-90°=55°,
∴∠COE=∠BOE=55°,
∴OE平分∠BOC.
点评 本题考查了角度的计算,理解角的平分线的定义以及互余的定义是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径.动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q两点同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t,求:
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径.动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q两点同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t,求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
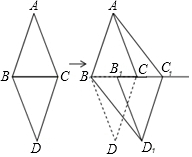 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为14cm.
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为14cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{33}{1296}$ | B. | $\frac{334}{1296}$ | C. | $\frac{343}{1296}$ | D. | $\frac{433}{1296}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
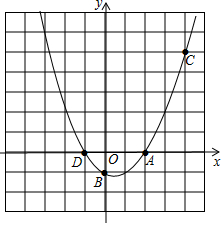 如图,已知二次函数y=ax2+bx+c经过点A(2,0),B(0,-1),C(4,5)三点.
如图,已知二次函数y=ax2+bx+c经过点A(2,0),B(0,-1),C(4,5)三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com