Question

已知抛物线y=ax²-3ax+4，
（1）求抛物线的对称轴；
（2）若抛物线与x轴交于A（-1，0）、B两点，且过第一象限上点D（m，m+1），求sin∠DAB．

Answer 1

分析：（1）根据抛物线的对称轴公式即可解答；
（2）将A（-1，0）代入y=ax²-3ax+4，求出抛物线解析式，进而求出B点坐标，将点D（m，m+1）代入抛物线解析式，求出m的值，再画出图形，根据三角函数的定义即可求出sin∠DAB的值．

解答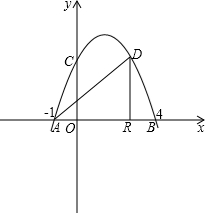：解：（1）抛物线的对称轴为x=-

-3a

2a

=

3

2

；

（2）将A（-1，0）代入y=ax²-3ax+4得，
a+3a+4=0，
解得a=-1，
解析式为y=-x²+3x+4．
当y=0时，原式可化为x²-3x-4=0，
解得x₁=-1，x₂=4．
则B点坐标为（4，0）．
将点D（m，m+1）代入y=-x²+3x+4得，
-m²+3m+4=m+1，
整理得，m²-2m-3=0，
解得m₁=-1，m₂=3．
则D点坐标为（-1，0）或（3，4）．
∵D（-1，0）与A点重合，故舍去．
则D（3，4）．
如图：因为D点坐标为（3，4），
所以OD=3，则AR=OA+OR=1+3=4，DR=4，
AD=

32+32

=3

2

．
sin∠DAB=sin∠DAR=

4

3 2

=

2 2

3

．

点评：此题考查了抛物线与x轴的交点与锐角三角函数的定义，求出抛物线解析式并画出草图是解题的关键．
而勾股定理也是重要解题工具．