
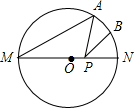
 如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )| A. | 4$\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 首先利用在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点P的位置,然后根据弧的度数发现一个等腰直角三角形计算.
解答 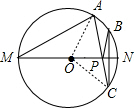 解:作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.
解:作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.
此时PA+PB最小,且等于AC的长.
连接OA,OC,
∵∠AMN=30°,
∴∠AON=60°,
∴弧AN的度数是60°,
则弧BN的度数是30°,
根据垂径定理得弧CN的度数是30°,
则∠AOC=90°,又OA=OC=2,
则AC=2$\sqrt{2}$.
故选C.
点评 此题主要考查了轴对称-最短路线问题,垂径定理,直角三角形的性质等,确定点P的位置是本题的关键.


科目:初中数学 来源: 题型:解答题

| 图① | 图② | 图③ | |
| 三个角上三个数的积 | 1×(-1)×2=-2 | (-3)×(-4)×(-5)=-60 | ② |
| 三个角上三个数的和 | 1+(-1)+2=2 | (-3)+(-4)+(-5)=-12 | ③ |
| 积与和的商 | (-2)÷2=-1 | ① | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com