
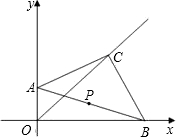
 ������B������Ϊ��6��0����
������B��������6��0����| 2 |
| 2 |
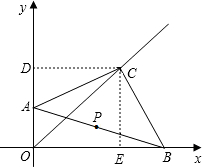 ���ACD+��ACE=90��
���ACD+��ACE=90��| 2 |
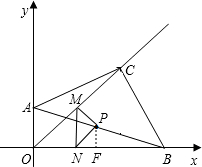
| (PF+MN)•NF |
| 2 |
| PF•NF |
| 2 |
| t2 |
| 2 |
| 3 |
| 2 |
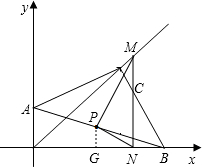
| (PG+MN)•NG |
| 2 |
| PG•NG |
| 2 |
| (1+t)(t-3) |
| 2 |
| t-3 |
| 2 |
| t(t-3) |
| 2 |
| t2 |
| 2 |
| 3t |
| 2 |
|


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
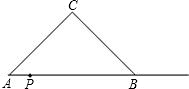 PQ=AP����PQΪһ��������������PQMN����������PQMN��Rt��ABC�ص����ֵ����ΪS��
PQ=AP����PQΪһ��������������PQMN����������PQMN��Rt��ABC�ص����ֵ����ΪS���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
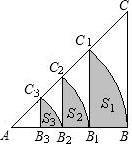 ��ͼ������Rt��ABC��ֱ�DZ߳�Ϊ4����AΪԲ�ģ�ֱ�DZ�ABΪ�뾶����BC1����б��AC�ڵ�C1��C1B1��AB�ڵ�B1���軡BC1��C1B1��B1BΧ�ɵ���Ӱ���ֵ����ΪS1��Ȼ����AΪԲ�ģ�AB1Ϊ�뾶����B1C2����б��AC�ڵ�C2��C2B2��AB�ڵ�B2���軡B1C2��C2B2��B2B1Χ�ɵ���Ӱ���ֵ����ΪS2�����˹��ɼ�������ȥ���õ�����Ӱ���ֵ����S3=
��ͼ������Rt��ABC��ֱ�DZ߳�Ϊ4����AΪԲ�ģ�ֱ�DZ�ABΪ�뾶����BC1����б��AC�ڵ�C1��C1B1��AB�ڵ�B1���軡BC1��C1B1��B1BΧ�ɵ���Ӱ���ֵ����ΪS1��Ȼ����AΪԲ�ģ�AB1Ϊ�뾶����B1C2����б��AC�ڵ�C2��C2B2��AB�ڵ�B2���軡B1C2��C2B2��B2B1Χ�ɵ���Ӱ���ֵ����ΪS2�����˹��ɼ�������ȥ���õ�����Ӱ���ֵ����S3=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
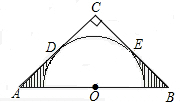 ��ͼ������Rt��ABC��б��AB=4��O��AB���е㣬��OΪԲ�ĵİ�Բ�ֱ������������ڵ�D��E��ͼ����Ӱ���ֵ�����Ƕ��٣���������������������æб�ʾ��
��ͼ������Rt��ABC��б��AB=4��O��AB���е㣬��OΪԲ�ĵİ�Բ�ֱ������������ڵ�D��E��ͼ����Ӱ���ֵ�����Ƕ��٣���������������������æб�ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
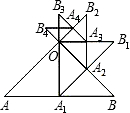 ��֪����ͼ������Rt��OAB��ֱ�DZ�OA�ij�Ϊ1����AB���ϵĸ�OA1Ϊֱ�DZߣ�����ʱ�뷽��������Rt��OA1B1��A1B1��OB�ཻ�ڵ�A2��������OA2Ϊֱ�DZ߰���ʱ�뷽��������Rt��OA2B2��A2B2��OB1�ཻ�ڵ�A3����������������ȥ���õ���OA3B3����OA4B4���������OA6B6���ܳ���
��֪����ͼ������Rt��OAB��ֱ�DZ�OA�ij�Ϊ1����AB���ϵĸ�OA1Ϊֱ�DZߣ�����ʱ�뷽��������Rt��OA1B1��A1B1��OB�ཻ�ڵ�A2��������OA2Ϊֱ�DZ߰���ʱ�뷽��������Rt��OA2B2��A2B2��OB1�ཻ�ڵ�A3����������������ȥ���õ���OA3B3����OA4B4���������OA6B6���ܳ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
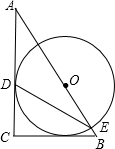 ��ͼ������Rt��ABC��AC=BC����б��AB�е�OΪԲ������O��AC�������ڵ�D����AB�ڵ�E������DE��
��ͼ������Rt��ABC��AC=BC����б��AB�е�OΪԲ������O��AC�������ڵ�D����AB�ڵ�E������DE���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com