(1)证明:∵正方形ABCD,
∴∠DAB=∠D=∠DCB=90°,
即AB=BC=CD=AD,AB⊥AD,BC⊥CD,
∴DA和CD都是圆B的切线,
∵PQ切圆B于F,
∴AP=PF,QF=CQ,
∴△DPQ的周长是DP+DQ+PQ=DP+DQ+PF+QF=DP+AP+DQ+CQ=AD+CD,
∵正方形ABCD的周长是AD+AB+CD+BC=2AD+2CD,
∴△DPQ的周长等于正方形ABCD的周长的一半.
(2)解:在Rt△PDQ中,由勾股定理得:DP
2+DQ
2=PQ
2,
∴(4-x)
2+(4-CQ)
2=(X+CQ)
2,
解得:CQ=

,
DQ=4-

=

,
∵正方形ABCD,
∴AD∥BC,
∴△PDQ∽△MCQ,
∴

=
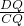
,
即

=

,
∴y=

+

x,
y与x之间的函数关系式是y=

+

x.
分析:(1)根据正方形性质得出AB⊥AD,BC⊥CD,推出DA和CB都是圆B的切线,根据切线长定理A得出PA=PF,QF=CQ,代入求出即可;
(2)在△DPQ中根据勾股定理求出CQ的值,求出DQ的值,根据平行线得出三角形相似,根据相似得出

=
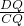
,代入求出即可.
点评:本题考查了勾股定理,切线的判定,切线长定理,相似三角形的性质和判定,正方形的性质等知识点的运用,能综合运用这些性质进行推理和计算是解此题的关键,题目综合性比较强,有一定的难度.

 ,F为
,F为 上的一动点,过点F作⊙B的切线交AD于点P,交DC于点Q.
上的一动点,过点F作⊙B的切线交AD于点P,交DC于点Q.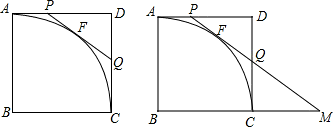
 ,
, =
= ,
, =
=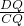 ,
, =
= ,
, +
+ x,
x, +
+ x.
x. =
=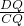 ,代入求出即可.
,代入求出即可.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案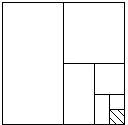 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
 在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.