

 ×5×100=250(m).
×5×100=250(m).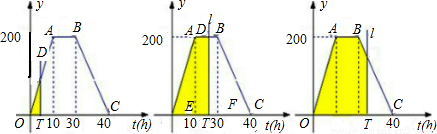
 •t•20t=10t2;
•t•20t=10t2; ×10×200+200(t-10)=200t-1000;
×10×200+200(t-10)=200t-1000; (20+40)×200-
(20+40)×200- (40-t)(-20t+800)=-10(40-t)2+6000;
(40-t)(-20t+800)=-10(40-t)2+6000;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 5、传说从前有一个虔诚的信徒,他是集市上的一个小贩.每天他都要从家所在的点A出发,到集市点B,但是,到集市之前他必须先拐弯到圆形古堡朝拜阿波罗神像.古堡是座圣城,阿波罗像供奉在古堡的圆心点O,而周围上的点都是供信徒朝拜的顶礼地点如图.这个信徒想,我怎样选择朝拜点,才能使从家到朝拜点,然后再到集市的路程最短呢?
5、传说从前有一个虔诚的信徒,他是集市上的一个小贩.每天他都要从家所在的点A出发,到集市点B,但是,到集市之前他必须先拐弯到圆形古堡朝拜阿波罗神像.古堡是座圣城,阿波罗像供奉在古堡的圆心点O,而周围上的点都是供信徒朝拜的顶礼地点如图.这个信徒想,我怎样选择朝拜点,才能使从家到朝拜点,然后再到集市的路程最短呢?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
(2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com