
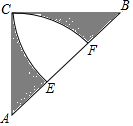
 如图,等腰直角三角形ABC中,∠C=90°,∠A=45°,直角边AC=BC=a,分别以点A点B为圆心以直角边为半径作弧交AB于点E,F.
如图,等腰直角三角形ABC中,∠C=90°,∠A=45°,直角边AC=BC=a,分别以点A点B为圆心以直角边为半径作弧交AB于点E,F.分析 (1)根据扇形面积公式即可求出扇形ACF的面积;
(2)由题意可知:阴影部分的面积为S△ABC-2(S△ABC-S扇形ACF)
(3)将a=2代入求值即可.
解答 解:(1)由题意可知扇形ACF的半径为a,圆心角度数为45°,
∴扇形ACF的面积为:$\frac{45°π{a}^{2}}{360°}$=$\frac{π{a}^{2}}{8}$;
(2)由题意可知:扇形BCE的面积为:$\frac{π{a}^{2}}{8}$
∴阴影部分的面积为:S△ABC-2(S△ABC-S扇形ACF)=$\frac{1}{2}$a2-2($\frac{1}{2}$a2-$\frac{π{a}^{2}}{8}$)=$\frac{π{a}^{2}}{4}$-$\frac{1}{2}$a2
(3)当a=2时,
∴$\frac{π{a}^{2}}{4}$-$\frac{1}{2}$a2=π-2=1.14
点评 本题考查扇形面积公式,涉及代入式化简求值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A、D、B、E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.请你判断上面这个判断是否正确,如果正确,请给出说明;如果不正确,请添加一个适当条件使它成为正确的判断,并加以说明.
如图,已知点A、D、B、E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.请你判断上面这个判断是否正确,如果正确,请给出说明;如果不正确,请添加一个适当条件使它成为正确的判断,并加以说明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com