
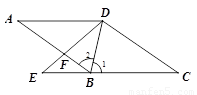
如图,四边形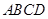 中,
中,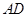 ∥
∥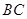 ,点
,点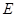 在
在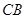 的延长线上,联结
的延长线上,联结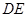 ,交
,交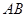 于点
于点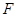 ,联结
,联结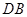 ,
,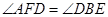 ,且
,且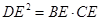 .
.
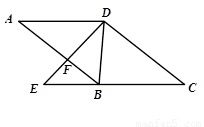
(1) 求证: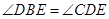 ;
;
(2)当 平分
平分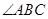 时,求证:四边形
时,求证:四边形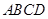 是菱形.
是菱形.
(1)、2)证明见解析
【解析】证明:(1)∵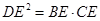 ,
,
∴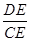 =
=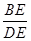 .
.
∵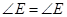 ,
,
∴△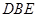 ∽△
∽△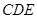 .
.
∴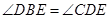 .
.
证明:(2)∵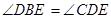 ,
,
又∵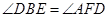 ,
,
∴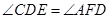 .
.
∴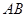 ∥
∥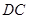 .
.
又∵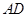 ∥
∥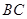 ,
,
∴四边形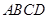 是平行四边形
是平行四边形
∵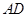 ∥
∥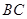 ,
,
∴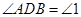 .
.
∵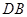 平分
平分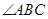 ,
,
∴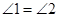 .
(1分)
.
(1分)
∴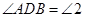 .
.
∴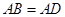 . (1分)
. (1分)
∴四边形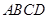 是菱形.
是菱形.
(1)先把等积式:DE2=BE•CE化为比例式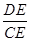 =
=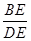 ,利用两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似证明△DBE∽△CDE即可证明∠DBE=∠CDE;
,利用两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似证明△DBE∽△CDE即可证明∠DBE=∠CDE;
(2)有(1)可知:∠DBE=∠CDE,利用角平分线的性质和平行线的判定以及平行四边形的判定方法证明四边形ABCD为平行四边形,再证明AB=AD即可证明:四边形ABCD是菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2012届上海市普陀区初三二模数学试卷(带解析) 题型:解答题
如图,四边形 中,
中,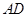 ∥
∥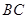 ,点
,点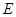 在
在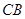 的延长线上,联结
的延长线上,联结 ,交
,交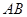 于点
于点 ,联结
,联结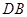 ,
,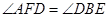 ,且
,且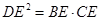 .
.
(1) 求证: ;
;
(2)当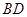 平分
平分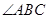 时,求证:四边形
时,求证:四边形 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏盐城卷)数学(带解析) 题型:填空题
如图,在四边形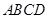 中,已知
中,已知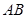 ∥
∥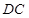 ,
,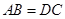 .在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是 .(填上你认为正确的一个答案即可)
.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是 .(填上你认为正确的一个答案即可)
查看答案和解析>>
科目:初中数学 来源:2011-2012学年常州市中考模拟考试数学卷 题型:解答题
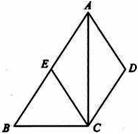
如图,四边形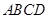 中,
中,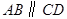 ,
,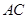 平分
平分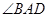 ,
,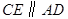 交
交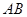 于
于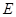 .
.
1.求证:四边形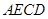 是菱形;
是菱形;
2.若点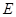 是
是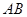 的中点,试判断
的中点,试判断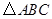 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com