
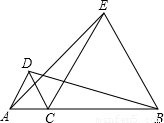
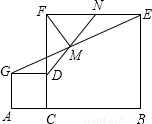
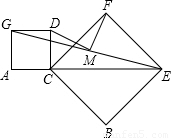
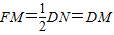 ,而NE=GD,GD=CD,可以推出NE=CD,∴FN=FD,可以得到FM⊥DM,所以DM与FM相等且垂直;
,而NE=GD,GD=CD,可以推出NE=CD,∴FN=FD,可以得到FM⊥DM,所以DM与FM相等且垂直;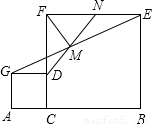 ∵EF∥GD,
∵EF∥GD, ,
,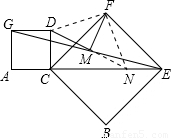 延长DM交CE于N,连接DF、FN,
延长DM交CE于N,连接DF、FN, DN,且FM⊥DN,
DN,且FM⊥DN,

科目:初中数学 来源:2009年5月湖北省随州市曾都区十校联考初三数学试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2009年5月湖北省随州市广水市十校联考初三数学试卷(解析版) 题型:解答题
 ”的游戏方案.
”的游戏方案.查看答案和解析>>
科目:初中数学 来源:2009年5月湖北省随州市广水市十校联考初三数学试卷(解析版) 题型:解答题
| 捐款(元) | 5 | 10 | 20 | 50 |
| 人数 | 6 | ?????? | 7 | |
查看答案和解析>>
科目:初中数学 来源:2009年5月湖北省随州市广水市十校联考初三数学试卷(解析版) 题型:选择题
 =
=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com