
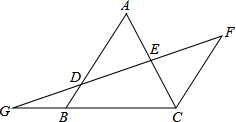
 如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
|


科目:初中数学 来源: 题型:
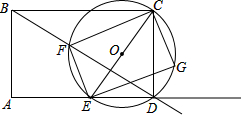 如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.
如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.查看答案和解析>>
科目:初中数学 来源: 题型:
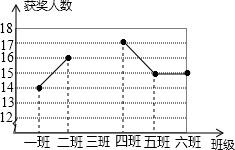 某中学组织网络安全知识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.
某中学组织网络安全知识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.查看答案和解析>>
科目:初中数学 来源: 题型:
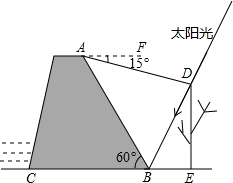 星期天,小强去水库大坝游玩,他站在大坝上的A处,看到一棵大树的影子刚好落在坝底的B处(假设大树DE与地面垂直,点A与大树及其影子在同一平面内),此时太阳光与地面成60°角;在A处测得树顶D的俯角为15°.如图所示,已知AB与地面的夹角为 60°,AB为12米.请你帮助小强计算一下这颗大树的高度?(结果精确到0.1米.参考数据:
星期天,小强去水库大坝游玩,他站在大坝上的A处,看到一棵大树的影子刚好落在坝底的B处(假设大树DE与地面垂直,点A与大树及其影子在同一平面内),此时太阳光与地面成60°角;在A处测得树顶D的俯角为15°.如图所示,已知AB与地面的夹角为 60°,AB为12米.请你帮助小强计算一下这颗大树的高度?(结果精确到0.1米.参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
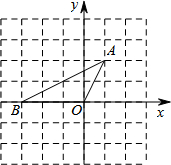 如图,把直角坐标系xoy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.
如图,把直角坐标系xoy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.查看答案和解析>>
科目:初中数学 来源: 题型:
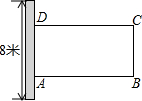 列方程(组)解应用题:
列方程(组)解应用题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com