
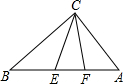
 如图,在直角的直角顶点C作斜边AB的三等分点的连线CE、CF,已知CE=sinα,CF=cosα(α为锐角),则边AB的长是多少?
如图,在直角的直角顶点C作斜边AB的三等分点的连线CE、CF,已知CE=sinα,CF=cosα(α为锐角),则边AB的长是多少?  口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
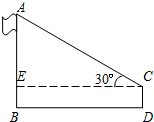 在学习了解直角三角形的有关知识后,一学习小组到操场测量学校旗杆的高度.如图,在测点D处安置测倾器,测得旗杆顶的仰角∠ACE的大小为30°,量得仪器的高CD为1.5米,测点D到旗杆的水平距离BD为18米,请你根据上述数据计算旗杆AB的高度(结果精确到0.1米;参考数据
在学习了解直角三角形的有关知识后,一学习小组到操场测量学校旗杆的高度.如图,在测点D处安置测倾器,测得旗杆顶的仰角∠ACE的大小为30°,量得仪器的高CD为1.5米,测点D到旗杆的水平距离BD为18米,请你根据上述数据计算旗杆AB的高度(结果精确到0.1米;参考数据| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
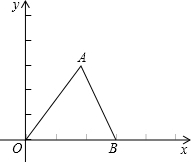 如图,在平面直角坐标系中,已知:△ABC的三个顶点的坐标分别是A(4,6)、B(0,0)、C(6,0).
如图,在平面直角坐标系中,已知:△ABC的三个顶点的坐标分别是A(4,6)、B(0,0)、C(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 2 |
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在等腰梯形ABCD中,AD∥BC,BC=![]() ,AD=
,AD=![]() ,∠B=450,直角三角板含450角的顶
,∠B=450,直角三角板含450角的顶
点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F。若△ABE为等腰三角形,则CF的长等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com