
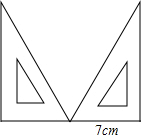
 用30°角的三角板作图形的平移运动)
用30°角的三角板作图形的平移运动)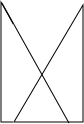
 ×42=4
×42=4 (cm2);
(cm2);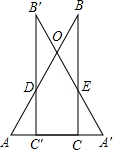 ∵AC=A′C′=7cm,
∵AC=A′C′=7cm, cm.
cm. ×102-
×102- ×3×3
×3×3 ×2=25
×2=25 -9
-9 =16
=16 (cm2);
(cm2);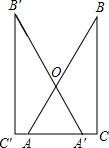
 x2;
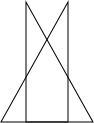
x2;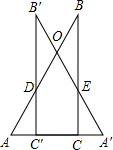 ②当14cm≥x≥7cm时,重叠部分是五边形ODC′CE,如右图,此时AA′=x.
②当14cm≥x≥7cm时,重叠部分是五边形ODC′CE,如右图,此时AA′=x. (x-7)cm.
(x-7)cm. x2-
x2- ×(x-7)×
×(x-7)× (x-7)×2=
(x-7)×2= x2-
x2- (x-7)2=-
(x-7)2=- x2+14
x2+14 x-49
x-49 .
.

科目:初中数学 来源: 题型:
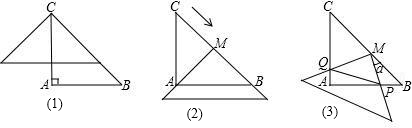
查看答案和解析>>
科目:初中数学 来源: 题型:
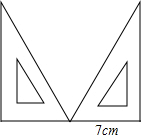 用30°角的三角板作图形的平移运动)
用30°角的三角板作图形的平移运动)查看答案和解析>>
科目:初中数学 来源: 题型:
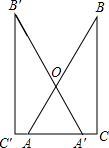
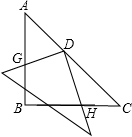 角形的斜边中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AB、BC上.
角形的斜边中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AB、BC上.查看答案和解析>>
科目:初中数学 来源:2012年浙江省绍兴市绍兴县夏履镇中学中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com