
(1)证明:∵AB∥CD,
∴∠1=∠B,
∵∠1=∠BPD+∠D,
∴∠BPD=∠B-∠D;
(2)不成立.∠BPD=∠B+∠D.
理由:过点P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠1+∠2=∠B+∠D;
(3)连接QP,并延长到E,
∵∠1=∠B+∠BQP,∠2=∠D+∠DQP,
∴∠BPD=∠1+∠2=∠BQP+∠B+∠DQP+∠D=∠B+∠D+∠BQD.
分析:(1)由AB∥CD,根据平行线的性质,易得∠1=∠B,又由三角形外角的性质可得:∠1=∠D+∠BPD,继而求得答案;
(2)首先过点P作PE∥AB,根据平行线的性质,可得∠1=∠B,∠2=∠D,继而证得∠BPD=∠B+∠D.
(3)首先连接QP,并延长到E,利用三角形外角的性质,可证得∠BPD=∠1+∠2=∠BQP+∠B+∠DQP+∠D=∠B+∠D+∠BQD.
点评:此题考查了平行线的性质以及三角形外角的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

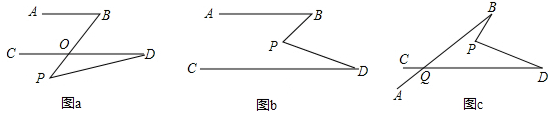
 (1)证明:∵AB∥CD,
(1)证明:∵AB∥CD,
