
如图所示,二次函数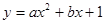 (
( )的图像与
)的图像与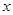 轴分别交于
轴分别交于 (
(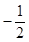 ,
, )、
)、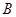 (
(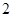 ,
, )两点,且与
)两点,且与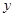 轴交于点
轴交于点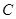 ;
;
(1)求该拋物线的解析式,并判断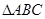 的形状;
的形状;
(2)在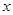 轴上方的拋物线上有一点
轴上方的拋物线上有一点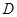 ,且以
,且以 、
、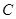 、
、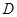 、
、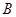 四点为顶点的四边形是等腰梯形,请直接写
四点为顶点的四边形是等腰梯形,请直接写
出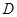 点的坐标;
点的坐标;
(3)在此拋物线上是否存在点P,使得以 、
、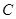 、
、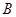 、
、 四点为顶点的四边形是直角梯形?若存在,求
四点为顶点的四边形是直角梯形?若存在,求
(4)出 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.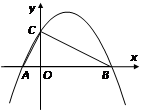
解:(1)根据题意,将 (
( ,
, ),
), (
(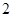 ,
, )代入
)代入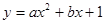 中,得
中,得 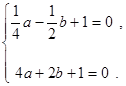 解这个方程,得
解这个方程,得 ,
,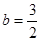 ,
,
∴ 该拋物线的解析式为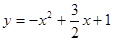 ,
,
当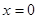 时,
时, ,
,
∴ 点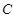 的坐标为(
的坐标为( ,
,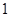 )。
)。
∴ 在 中,
中,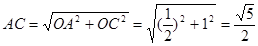 .
.
在 中,
中,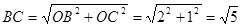 .
. , ∵
, ∵ 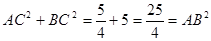 ,
,
∴ 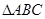 是直角三角形.
是直角三角形.
(2)点 的坐标为(
的坐标为( ,
,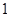 ).
).
(3)存在.
由(1)知,AC^BC.
①若以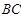 为底边,则
为底边,则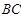 ∥
∥ ,如图1所示,
,如图1所示,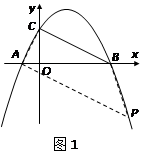
可求得直线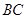 的解析式为
的解析式为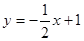 ,直线
,直线 可以看作是由直线
可以看作是由直线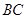 平移得到的,
平移得到的,
所以设直线 的解析式为
的解析式为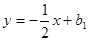 ,
,
把点 (
( ,
, )代入直线
)代入直线 的解析式,求得
的解析式,求得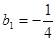 ,
,
∴ 直线 的解析式为
的解析式为 .
.
∵ 点 既在拋物线上,又在直线
既在拋物线上,又在直线 上,
上,
∴ 点 的纵坐标相等,即
的纵坐标相等,即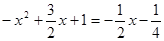 ,
,
解得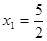 ,
,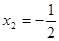 (舍去)。
(舍去)。
当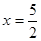 时,
时, ,
,
∴ 点 (
(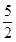 ,
, ).
).
②若以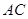 为底边,则
为底边,则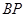 ∥
∥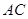 ,如图2所示.
,如图2所示.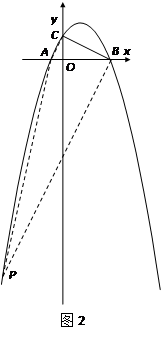
可求得直线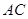 的解析式为
的解析式为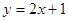 .直线
.直线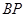 可以看作是由直线
可以看作是由直线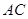 平移得到的,
平移得到的,
所以设直线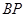 的解析式为
的解析式为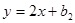 ,
,
把点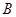 (
(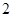 ,
, )代入直线
)代入直线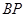 的解析式,求得
的解析式,求得 ,
,
∴ 直线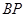 的解析式为
的解析式为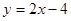 .
.
∵点 既在拋物线上,又在直线
既在拋物线上,又在直线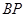 上,
上,
∴点 的纵坐标相等,<
的纵坐标相等,<
解析


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
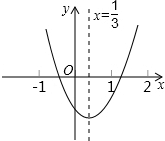 小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面六条信息:
小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面六条信息:| A、3个 | B、4个 | C、5个 | D、6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
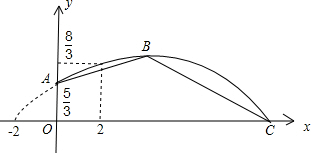 铅球从A点被推出,实线部分表示铅球所经过的路线)
铅球从A点被推出,实线部分表示铅球所经过的路线)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:| A、2个 | B、3个 | C、4个 | D、1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,二次函数 y=ax2+bx+c的图象与x轴交于点A和点B(A、B分别位于原点O的两侧),与y轴的下半轴交于点C,且tan∠OAC=2,AB=CB=5.
如图所示,二次函数 y=ax2+bx+c的图象与x轴交于点A和点B(A、B分别位于原点O的两侧),与y轴的下半轴交于点C,且tan∠OAC=2,AB=CB=5.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•甘谷县模拟)如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b+c=0;④当x=-1或x=3时,函数y的值都等于0.把正确结论的序号填在横线上
(2012•甘谷县模拟)如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b+c=0;④当x=-1或x=3时,函数y的值都等于0.把正确结论的序号填在横线上查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com