作一个图形关于一条直线的轴对称图形,再将这个轴对称图形沿着与这条直线平行的方向平移,我们把这样的图形变换叫做关于这条直线的滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1),结合轴对称和平移的有关性质,解答以下问题:
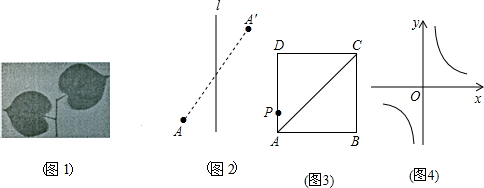
(1)如图2,在关于直线l的滑动对称变换中,试证明:两个对应点A,A′的连线被直线l平分;
(2)若点P是正方形ABCD的边AD上的一点,点P关于对角线AC滑动对称变换的对应点P′也在正方形ABCD的边上,请仅用无刻度的直尺在图3中画出P′;
(3)定义:若点M到某条直线的距离为d,将这个点关于这条直线的对称点N沿着与这条直线平行的方向平移到点M′的距离为s,称[d,s]为点M与M′关于这条直线滑动对称变换的特征量.如图4,在平面直角坐标系xOy中,点B是反比例函数y=
的图象在第一象限内的一个动点,点B关于y轴的对称点为C,将点C沿平行于y轴的方向向下平移到点B′.
①若点B(1,3)与B′关于y轴的滑动对称变换的特征量为[m,m+4],判断点B′是否在此函数的图象上,为什么?
②已知点B与B′关于y轴的滑动对称变换的特征量为[d,s],且不论点B如何运动,点B′也都在此函数的图象上,判断s与d是否存在函数关系?如果是,请写出s关于d的函数关系式.




 优百分课时互动系列答案
优百分课时互动系列答案