实数a,b,c满足a≤b≤c,且ab+bc+ca=0,abc=1.求最大的实数k,使得不等式|a+b|≥k|c|恒成立.
解:不等式|a+b|≥4|c|对满足题设条件的实数a,b,c恒成立.由已知条件知,a,b,c都不等于0,且c>0.
因为abc=1,有ab=

>0;
又因为ab+bc+ca=0,
所以a+b=-
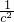
<0,
所以a≤b<0.
由一元二次方程根与系数的关系知,a,b是一元二次方程x
2+
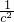
x+

=0的两个实数根,
于是△=
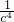
-
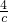
≥0,
所以c
3≤

.
因此|a+b|=-(a+b)=
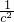
≥4c=4|c|,不等式|a+b|≥4|c|对满足题设条件的实数a,b,c恒成立,
所以k≤4,最大的实数k为4.
分析:通过实数a,b,c满足a≤b≤c,且ab+bc+ca=0,abc=1,利用c表示a+b和ab,并且确定它们的符号.然后写出以a、b为根的一元二次方程,则有△≥0,得到c的范围,再变形|a+b|,有|a+b|=-(a+b)=
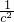
≥4c=4|c|,最后确定k的范围,找到k的最大值.
点评:本题考查了一元二次方程根的判别式.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.也考查了一元二次方程根与系数的关系,以a,b两数为根的方程为:x
2+(a+b)x+ab=0.熟练掌握不等式的性质和绝对值的含义.

 >0;
>0;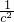 <0,
<0,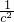 x+
x+ =0的两个实数根,
=0的两个实数根,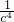 -
-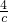 ≥0,
≥0, .
.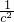 ≥4c=4|c|,不等式|a+b|≥4|c|对满足题设条件的实数a,b,c恒成立,
≥4c=4|c|,不等式|a+b|≥4|c|对满足题设条件的实数a,b,c恒成立,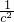 ≥4c=4|c|,最后确定k的范围,找到k的最大值.
≥4c=4|c|,最后确定k的范围,找到k的最大值.
