
�ٶ� (ǧ��/ʱ) (ǧ��/ʱ) | 0 | 5 | 10 | 15 | 20 | 25 | �� |
ɲ������ (��) (��) | 0 |  | 2 |  | 6 |  | �� |
 ��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������
��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������ (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
(ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
 (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)���㺯��
(ǧ��/ʱ)���㺯�� ������������ٶȷ��������ײԭ��
������������ٶȷ��������ײԭ�� 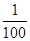 x2+
x2+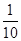 x��
x�� ,����ٶ�
,����ٶ� (ǧ��/ʱ)������Ϊ40ǧ��/ʱ�ȽϷ�����ײԭ��.
(ǧ��/ʱ)������Ϊ40ǧ��/ʱ�ȽϷ�����ײԭ��.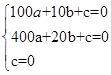 ���
���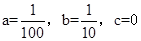
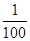 x2+
x2+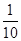 x��
x�� 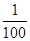 x2+
x2+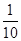 x=12�����x1=��40����ȥ����x2=30��
x=12�����x1=��40����ȥ����x2=30��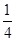 x�����x=42��
x�����x=42��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ,0)ΪԲ�ģ���
,0)ΪԲ�ģ��� Ϊ�뾶Բ��x���ཻ�ڵ�B��C����y���ཻ�ڵ�D��E.
Ϊ�뾶Բ��x���ཻ�ڵ�B��C����y���ཻ�ڵ�D��E.
 ������C��D���㣬�������ߵĽ���ʽ�����жϵ�B�Ƿ��ڸ��������ϣ�
������C��D���㣬�������ߵĽ���ʽ�����жϵ�B�Ƿ��ڸ��������ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
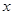 �ύ��
�ύ��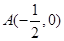 ,
,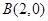 ���㣬����
���㣬����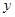 �ύ�ڵ�
�ύ�ڵ�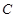 .
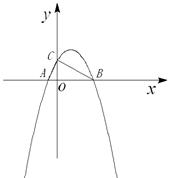
.
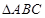 ����״Ϊ ��
����״Ϊ ��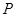 ,ʹ����
,ʹ����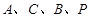 �ĵ�Ϊ������ı��������Σ���
�ĵ�Ϊ������ı��������Σ���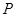 �������Ϊ .
�������Ϊ .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
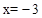 ���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N����
���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N���� ��
��
 ��������
�������� ��x�����һ����ΪA��BΪ������
��x�����һ����ΪA��BΪ������ �Ϻ�����Ϊ2�ĵ㡣
�Ϻ�����Ϊ2�ĵ㡣�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
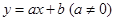 ��ͼ����
��ͼ����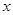 ��Ľ�������Ϊ(��2��0)����������
��Ľ�������Ϊ(��2��0)����������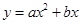 �ĶԳ���Ϊ( )
�ĶԳ���Ϊ( )| A��ֱ��x=1 | B��ֱ��x=��2 | C��ֱ��x=��1 | D��ֱ��x=��4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com