Question

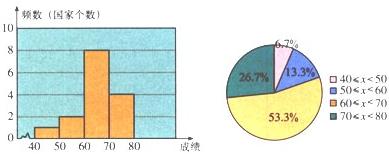
下面是1998年参加国际教育评估的15个国家学生的数学平均成绩（x）：
40　51　56　61　62
66　62　68　65　64
69　70　77　76　78
（1）取组距为10并按照上限不在内的原则分组统计，列出频数分布表并画出频数分布直方图；
（2）写出一条可以得到的结论．

Answer 1

解：（1）①决定极差，本组数据中最大的数是78，最小的数是40
∴极差=78-40=38
②决定组距与组数
条件告诉组距为10，∴组数为：38÷10=3.8，应该为4个组
③决定分点
为了不让某些数在分点上，可以使分点比原数多一位小数，即为：39.5～49.5，49.5～59.5，59.5～69.5，69.5～79.5，
④画出频数分布表为：

平均成绩（x）	划记	频数
39.5≤x＜49.5	一	1
49.5≤x＜59.5		2
59.5≤x＜69.5	正	8
69.5≤x＜79.5		4
合计		15

⑤画频数分布直方图为：


（2）从上面的统计表和直方图可以看出：
平均成绩在69.5～79.5国家最多，有8个国家．
分析：（1）先找到最大数78和最小数40，求出极差是38，再决定组数38÷10=3.8，应该为4个组，再决定分点，为了不让某些数在分点上，可以使分点比原数多一位小数，即为：39.5～49.5，49.5～59.5，59.5～69.5，69.5～79.5，根据分组就可以列出频数分布表和画出频数分布直方图．
（2）由（1）的直方图或统计表的数据及变化规律就可以得出一个相应的结论，看出成绩在那个分数段的人数最多．
点评：本题考查了画频数分布表和频数分布直方图的方法以及根据数据总结一般结论的能力．