练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知函数，其中

    若在x=1处取得极值，求a的值；

    求的单调区间；

    （Ⅲ）若的最小值为1，求a的取值范围。  

     解（Ⅰ）

    ∵在x=1处取得极值，∴解得

    （Ⅱ）

    ∵     ∴

    ①当时，在区间∴的单调增区间为

    ②当时，

    由

    ∴

    （Ⅲ）当时，由（Ⅱ）①知，

    当时，由（Ⅱ）②知，在处取得最小值

    综上可知，若得最小值为1，则a的取值范围是

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知：如图，在平面直角坐标系内，直线y=
    3
    4
    x上有一点A，AD⊥x轴于D，且AD=3，C是x轴上的一点，AC⊥AO，长度等于OD的线段EF在x轴上沿OC方向以1/s的速度向点C运动（运动前EF和OD重合，当F点与C重合时停止运动，包括起点、终点），过E，F分别作OC的垂线交直角边于点P、点Q，连接线段PD，QD，PQ，PQ交线段AD于点M，若设EF运动的时间为t（s）．
    （1）写出A点坐标
     
    ．PE=
     
    （用含t的代数式表示线段），其中自变量t的取值范围为
     
    ；
    （2）是否存在t的值，使得线段PD⊥QD？若存在，请求出相应的t的值，若不精英家教网存在，请说明理由；
    （3）①当t=
    4
    5
    秒时，线段AM=
     
    ；
    ②求线段AM关于自变量t的函数解析式，并求出AM的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知抛物线（其中）．

    1.（1）求该抛物线与x轴的交点坐标及顶点坐标(可以用含k的代数式表示)；

    2.（2）若记该抛物线的顶点坐标为，直接写出的最小值；

    3.（3）将该抛物线先向右平移个单位长度，再向上平移个单位长度，随着的变化，平移后的抛物线的顶点都在某个新函数的图象上，求这个新函数的解析式（不要求写自变量的取值范围）．

     

    查看答案和解析>>

    科目：初中数学 来源：2011届北京市大兴区初三第一学期期末数学卷 题型：解答题

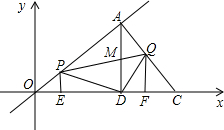
    已知抛物线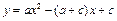（其中a ≠ c且a ≠0）.
    （1）求此抛物线与x轴的交点坐标；（用a，c的代数式表示）
    （2）若经过此抛物线顶点A的直线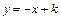与此抛物线的另一个交点为，
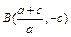    求此抛物线的解析式；
    （3）点P在（2）中x轴上方的抛物线上，直线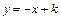与 y轴的交点为C，若
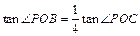    ，求点P的坐标；
    （4）若（2）中的二次函数的自变量x在n≤x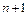＜（n为正整数）的范围内取值时，记它的整数函数值的个数为N， 则N关于n的函数关系式为        .

    查看答案和解析>>

    科目：初中数学 来源：2012届北京市西城区九年级第一学期期末测试数学卷 题型：解答题

    已知抛物线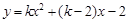（其中）．

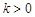    1.（1）求该抛物线与x轴的交点坐标及顶点坐标(可以用含k的代数式表示)；

    2.（2）若记该抛物线的顶点坐标为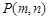，直接写出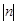的最小值；

    3.（3）将该抛物线先向右平移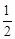个单位长度，再向上平移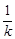个单位长度，随着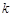的变化，平移后的抛物线的顶点都在某个新函数的图象上，求这个新函数的解析式（不要求写自变量的取值范围）．

     

    查看答案和解析>>

    同步练习册答案