
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
| 项目 品牌 | 单价/元 | 购买数量/台 | 购买费用/元 |
| A | 800 | x | 800x |
| B | 1000 | 120-x | 1000(120-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1项 | B. | 2项 | C. | 3项 | D. | 4项 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+2xy+4y2 | B. | 25m2+10mn+n2 | C. | a2+ab+b2 | D. | x2-2xy-$\frac{1}{4}$y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${({\frac{1}{3}})^5}$米 | B. | ${({\frac{2}{3}})^5}$米 | C. | $[{1-{{({\frac{1}{3}})}^5}}]$米 | D. | $[{1-{{({\frac{2}{3}})}^5}}]$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走( )米才最理想.
主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走( )米才最理想.| A. | 18-6$\sqrt{5}$ | B. | 6$\sqrt{5}$-6 | C. | 6$\sqrt{5}$+6 | D. | 18-6$\sqrt{5}$或6$\sqrt{5}$-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
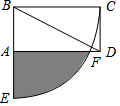 如图,已知矩形ABCD中,AB=1 cm,BC=2 cm,以B为圆心,BC为半径作$\frac{1}{4}$圆弧交AD于点F,交BA的延长线于点E,则扇形BCE被矩形所截剩余部分的面积为$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.
如图,已知矩形ABCD中,AB=1 cm,BC=2 cm,以B为圆心,BC为半径作$\frac{1}{4}$圆弧交AD于点F,交BA的延长线于点E,则扇形BCE被矩形所截剩余部分的面积为$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两边和一角对应相等的两个三角形全等 | |
| B. | 垂直于同一条直线的两直线平行 | |
| C. | 内错角相等 | |
| D. | 有一个角是60°的等腰三角形是等边三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com