说理,填空(在括号中填上相应的依据)
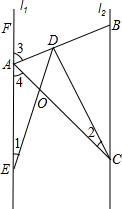
已知:l
1∥l
2,∠CAB=∠CBA,∠ACB=∠CDE
求证:AB平分∠CAF;∠1=∠2.
证明如下:
∵l
1∥l
2(已知)
∴∠CBA=∠3(
两直线平行,内错角相等
两直线平行,内错角相等
)
∵∠CAB=∠CBA(已知)
∴∠3=∠CAB
∴AB平分∠CAF(
角平分线定义
角平分线定义
)
∵l
1∥l
2(已知)
∴∠ACB=∠4(
两直线平行,内错角相等
两直线平行,内错角相等
)
又∵∠ACB=∠CDE(已知)
∴∠4=∠CDE(
等量代换
等量代换
)
又∵∠4+∠1+∠AOE=180°
∠2+∠CDE+∠DOC=180°(
三角形内角和定理
三角形内角和定理
)
∴∠4+∠1+∠AOE=∠2+∠CDE+∠DOC(
等量代换
等量代换
)
∵∠4=∠CDE(已证),∠AOE=∠DOC(
已证
已证
)
∴∠1=∠2.

 说理,填空(在括号中填上相应的依据)
说理,填空(在括号中填上相应的依据)
