
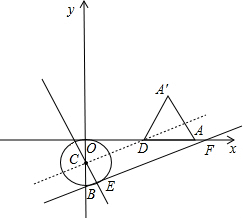
 ,0),直线y=(2-
,0),直线y=(2- )x-2交x轴于点F,y轴于点B,直线l∥AB且交 y轴于点C,交x轴于点D,点A关于直线l的对称点为A',连接AA',A'D.直线l从AB开始,以1个单位每秒的速度沿y轴正方向向上平移,设移动时间为t.
)x-2交x轴于点F,y轴于点B,直线l∥AB且交 y轴于点C,交x轴于点D,点A关于直线l的对称点为A',连接AA',A'D.直线l从AB开始,以1个单位每秒的速度沿y轴正方向向上平移,设移动时间为t. )x-2于点E,以点C为圆心CE为半径作⊙C,求当t为何值时,⊙C与△AA′D三边所在直线相切?
)x-2于点E,以点C为圆心CE为半径作⊙C,求当t为何值时,⊙C与△AA′D三边所在直线相切?
 解:(1)∵l∥AB.
解:(1)∵l∥AB. ,0)B(0,-2),
,0)B(0,-2), ,
, (2-t),
(2-t), t.
t. t∠A'DA=60°,
t∠A'DA=60°, tA'H=
tA'H= t,
t, -
- t,
t, t).
t).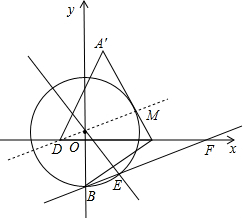
 ,0),
,0), ,OB=2,
,OB=2, t,
t, .
. ,0),求出∴∠ODC=∠OAB=30°由点A关于直线l的对称点为A',求出A'点的坐标(用t的代数式表示);
,0),求出∴∠ODC=∠OAB=30°由点A关于直线l的对称点为A',求出A'点的坐标(用t的代数式表示); ,OB=2,求出AB,得AB=AF;
,OB=2,求出AB,得AB=AF;

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2005年重庆市中考数学试卷(课标卷)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com