
 如图,正方形DECF内接于Rt△ABC中,D在斜边AB上,且AD=4cm,BD=3cm,则图中阴影部分的面积为_____cm2.
如图,正方形DECF内接于Rt△ABC中,D在斜边AB上,且AD=4cm,BD=3cm,则图中阴影部分的面积为_____cm2.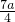 ,AC=
,AC=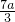 ,在Rt△ABC中,利用勾股定理得到a=
,在Rt△ABC中,利用勾股定理得到a= ,于是得到BC=
,于是得到BC=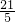 ,AC=
,AC=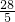 ,而S阴影部分=S△ACB-S正方形ECFD,运用三角形和正方形的面积公式即可得到答案.
,而S阴影部分=S△ACB-S正方形ECFD,运用三角形和正方形的面积公式即可得到答案.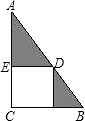 解:设正方形的边长为a,
解:设正方形的边长为a,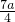 ,AC=
,AC=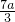 ,
,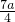 )2+(
)2+(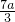 )2=72,
)2=72, ,
,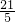 ,AC=
,AC=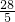 ,
, ×
×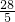 ×
×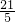 -(
-( )2=6(cm2).
)2=6(cm2).

科目:初中数学 来源: 题型:
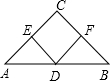 如图Rt△ABC中,D斜边AB的中点,过D分别作DE⊥AC,DF⊥BC,垂足为E,F,则四边形DECF是正方形还需添加的条件是
如图Rt△ABC中,D斜边AB的中点,过D分别作DE⊥AC,DF⊥BC,垂足为E,F,则四边形DECF是正方形还需添加的条件是查看答案和解析>>
科目:初中数学 来源: 题型:
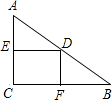 如图,在Rt△ABC中,∠C=90°,DE垂直平分AC,DF⊥BC,当△ABC满足条件
如图,在Rt△ABC中,∠C=90°,DE垂直平分AC,DF⊥BC,当△ABC满足条件查看答案和解析>>
科目:初中数学 来源: 题型:
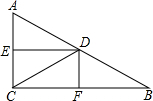 如图,Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、BC的中点,连接DE、DF、CD,如果
如图,Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、BC的中点,连接DE、DF、CD,如果查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com