
| A. | -7 | B. | 2 | C. | 9 | D. | 18 |
分析 设a+b=m,则ab=m+3,a2+b2变形,再整体代入,转化为关于x的二次函数求最小值,注意a、b正实数的条件的运用.
解答 解:设a+b=m,则ab=m+3,
a、b可看作关于x的方程x2-mx+m+3=0的两根,
a、b为实数,则△=(-m)2-4(m+3)≥0,
解得m≤-2或m≥6,而a、b为正实数,
∴a+b=m>0,只有m≥6,
∴a2+b2=(a+b)2-2ab=m2-2(m+3)=(m-1)2-7,
可知当m≥1时,a2+b2随m的增大而增大,
∴当m=6时,a2+b2的值最小,为18.
故选D.
点评 本题考查了二次函数最值在确定代数式的值中的运用.本题要注意:①根据已知条件换元,转化为二次函数,②a、b为正实数条件的运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
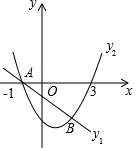 如图,A(-1,0)、B(2,-3)两点在一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象上.
如图,A(-1,0)、B(2,-3)两点在一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
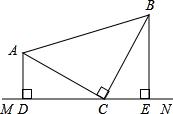 如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN,BE⊥MN,垂足分别为点D,E.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN,BE⊥MN,垂足分别为点D,E.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.| 剪的次数 | 1 | 2 | 3 | 4 | 5 |
| 正方形个数 | 4 | 7 | 10 | 13 | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com