
【题目】如图,在三角形![]() 中,
中,![]() .将三角形
.将三角形![]() 绕着点
绕着点![]() 旋转,使得点
旋转,使得点![]() 落在直线
落在直线![]() 上的点
上的点![]() ,点
,点![]() 落在点
落在点![]() .
.
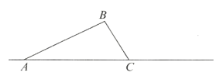
(1)画出旋转后的三角形![]() .
.
(2)求线段![]() 在旋转的过程中所扫过的面积(保留
在旋转的过程中所扫过的面积(保留![]() ).
).
(3)如果在三角形![]() 中,
中,![]() (其中
(其中![]() ).其他条件不变,请你用含有
).其他条件不变,请你用含有![]() 的代数式,直接写出线段
的代数式,直接写出线段![]() 旋转的过程中所扫过的面积(保留
旋转的过程中所扫过的面积(保留![]() ).
).
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
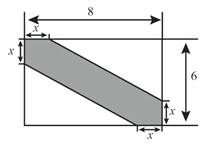
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
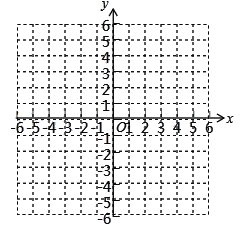
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出三角形ABC;
(2)若三角形ABC内有一点P(![]() ,
,![]() )经平移后对应点为P1(
)经平移后对应点为P1(![]() ,
,![]() ),将三角形ABC作同样的平移得到三角形A1B1C1,画出平移后的三角形A1B1C1,并直接写出点A1,B1,C1的坐标;
),将三角形ABC作同样的平移得到三角形A1B1C1,画出平移后的三角形A1B1C1,并直接写出点A1,B1,C1的坐标;
(3)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
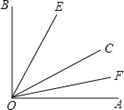
(1)若∠AOB=90°,∠AOC=30°,求∠EOF的度数;
(2)若∠AOB=![]() ,求∠EOF的度数(写出求解过程);
,求∠EOF的度数(写出求解过程);
(3)若将条件中“OE平分∠BOC,OF平分∠AOC.平分”改为“∠EOB=![]() ∠COB,∠COF=
∠COB,∠COF=![]() ∠COA”,且∠AOB=
∠COA”,且∠AOB=![]() ,求∠EOF的度数(写出求解过程).
,求∠EOF的度数(写出求解过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产480个零件.当生产任务完成一半时,停止生产进行反思和改进,用时20分钟.恢复生产后工作效率比原来可以提高20%,要求比原计划提前40分钟完成任务,那么反思改进后每小时需要生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
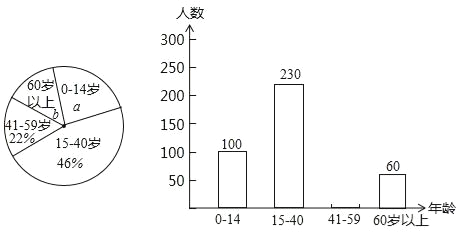
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,点O为坐标原点,点A在x轴正半轴上,点C在第一象限,且∠COA=60°,以OA、OC为邻边作菱形OABC,且菱形OABC的面积为![]() .
.
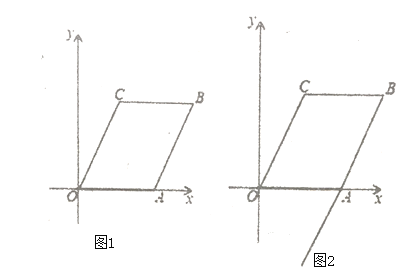
(1)求B. C两点的坐标;
(2)动点P从C点出发沿射线CB匀速运动,同时动点Q从A点出发沿射线BA的方向匀速运动,P、Q两点的运动速度均为2个单位/秒,连接PQ和AC,PQ和AC所在直线交于点D,点E为线段BQ的中点,连接DE,设动点P、Q的运动时间为t,请将△DQE的面积S用含t的式子表示,并直接写出t的取值范围;
(3)在(2)的条件下,过点Q作QF⊥y轴于点F,当t为何值时,以P、B.、F.、Q为顶点的四边形为平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料![]() :我们知道,如果一个三角形的三边长固定,那么这个三角形就固定。若给出任意一个三角形的三边长,你能求出它的面积吗?设一个三角形的三边长分别为
:我们知道,如果一个三角形的三边长固定,那么这个三角形就固定。若给出任意一个三角形的三边长,你能求出它的面积吗?设一个三角形的三边长分别为![]() ,
,![]() ,
,![]() ,我们把它的面积记为
,我们把它的面积记为![]() ,古希腊的几何学家海伦(Hcron,约公元50年),在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了一个通过三角形的三边长来求面积的海伦公式。我们可以把海伦公式变形为:
,古希腊的几何学家海伦(Hcron,约公元50年),在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了一个通过三角形的三边长来求面积的海伦公式。我们可以把海伦公式变形为:![]() (其中
(其中![]() )
)
材料2:把形如![]() 的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即![]() .配方法是中学数学的重要方法,用配方法可求最最大(小)值.
.配方法是中学数学的重要方法,用配方法可求最最大(小)值.
例如:求![]() 的最小值.
的最小值.
![]()
![]()
![]()
![]()
![]()
当![]() 时,
时,![]() ,此时
,此时![]() 取得最小值
取得最小值![]() ,
,
请你运用材料提供的方法,解答以下问题:
(1)若三角形的三边长分别为![]() ,
,![]() ,
,![]() ,求该三角形的面积;
,求该三角形的面积;
(2)小新手里有一根长![]() 米的铁丝,他想用这根铁丝制作一个三角形模型,要求该三角形的一边长为
米的铁丝,他想用这根铁丝制作一个三角形模型,要求该三角形的一边长为![]() 米且面积最大,请你帮助他计算出这个三角形另两边的边长,并说明理由.
米且面积最大,请你帮助他计算出这个三角形另两边的边长,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
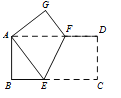
A. AF=AE B. △ABE≌△AGF C. EF=![]() D. AF=EF
D. AF=EF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com