
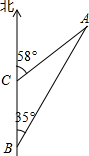
 如图,海中有一小岛,它周围8海里内有暗礁,渔船跟踪渔群由南向北航行,在B点测得小岛A在北偏东35°方向,航行12海里到达C点,测得小岛A在北偏东58°方向.如果渔船不改变航向,继续向北航行,有没有触礁的危险?(tan35°≈0.7002,tan581°≈1.6003,精确到0.1海里)
如图,海中有一小岛,它周围8海里内有暗礁,渔船跟踪渔群由南向北航行,在B点测得小岛A在北偏东35°方向,航行12海里到达C点,测得小岛A在北偏东58°方向.如果渔船不改变航向,继续向北航行,有没有触礁的危险?(tan35°≈0.7002,tan581°≈1.6003,精确到0.1海里) 分析 过点A作AD⊥BC于点D,解RT△ABD和Rt△ACD,求出AD=tan35°•BD=tan58°•DC,然后根据BD=12+DC,即可求得DC,进而求得AD.
解答 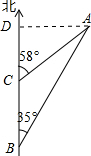 解:如果渔船不改变航线继续向北航行,没有触礁的危险,理由如下:
解:如果渔船不改变航线继续向北航行,没有触礁的危险,理由如下:
过点A作AD⊥BC,垂足为D.
在Rt△ABD中,∠ADB=90°,∠ABD=35°,
∴tan∠ABD=$\frac{AD}{BD}$,
∴AD=tan35°•BD,
在Rt△ACD中,∠ADC=90°,∠ACD=58°,∴tan∠ACD=$\frac{AD}{DC}$,
∴AD=tan58°•DC,
∴0.7BD=1.6DC,
∵BD=12+DC,
∴0.7(12+DC)=1.6DC,
∴DC=9.33,
∴AD=tan58°•DC=1.6×9,33≈14.9>8
∴渔船不改变航线继续向北航行,没有触礁的危险.
点评 本题考查了解直角三角形的应用,难度适中.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x+2}$ | B. | y=4x | C. | y=$\frac{2}{3x}$ | D. | y=$\frac{7}{x^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com