
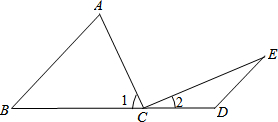
 如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.
如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2. (180°-∠B)=
(180°-∠B)= (180°-40°)=70°
(180°-40°)=70°  (180°-∠D)=
(180°-∠D)= (180°-140°)=20°;
(180°-140°)=20°; (180°-∠B)=90°-
(180°-∠B)=90°- ∠B
∠B  〔180°-∠D〕=
〔180°-∠D〕= 〔180°-(180°-∠B)〕=
〔180°-(180°-∠B)〕= ∠B,
∠B, ∠B+
∠B+ ∠B)=90°,
∠B)=90°, (180°-∠B)=90°-
(180°-∠B)=90°- ∠B,再根据平行线的性质得出∠B+∠D=180°,在△CDE中,根据∠D+∠E+∠2=180°,∠E=∠2可得出∠2=
∠B,再根据平行线的性质得出∠B+∠D=180°,在△CDE中,根据∠D+∠E+∠2=180°,∠E=∠2可得出∠2= ∠B,故∠ACE=180°-(∠1+∠2)=180°-(90°-
∠B,故∠ACE=180°-(∠1+∠2)=180°-(90°- ∠B+
∠B+ ∠B)=90°,由此即可得出结论.
∠B)=90°,由此即可得出结论.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.
如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2015届江苏省南京市高淳区七年级下学期期中质量调研检测数学试卷(解析版) 题型:解答题
如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.
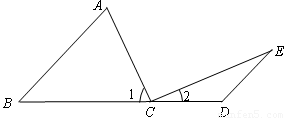
(1)若∠B=40°,求∠1、∠2的度数;
(2)判断AC与CE的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2014届江苏徐州市八年级下学期5月月考数学卷(解析版) 题型:填空题
如图,点C在线段BD上,AB⊥BD,PD⊥BD,∠B=∠D=90°,AB=3,BC=6,CD=2,则当DE= 时,△ABC与△CDE相似.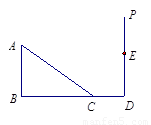
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com