
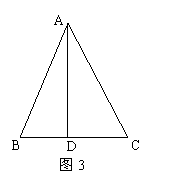
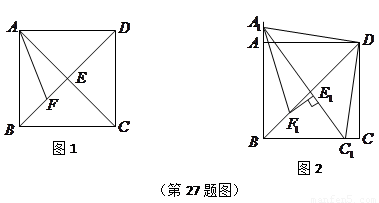
如图1,在正方形![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求证:![]() ;
;
(2)在图1中,若![]() 在
在![]() 上,且
上,且![]() ,则
,则![]() 成立吗?为什么?
成立吗?为什么?
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题:
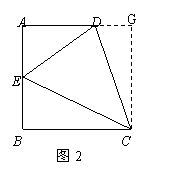
①如图2,在直角梯形ABCD中,![]() ∥
∥![]()
![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,且∠DCE=45°,求DE的长;
的中点,且∠DCE=45°,求DE的长;
②如图3,在△ABC中,∠BAC=45°,AD⊥BC,![]() ,则
,则
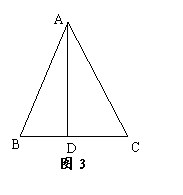

![]() 的面积为 (直接写出结果,不需要写出计算过程).
的面积为 (直接写出结果,不需要写出计算过程).
 |
证明:(1)在正方形ABCD中
 CB=CD, ∠B=∠CDA=90°
CB=CD, ∠B=∠CDA=90°
∴∠CDF=∠B =90°
∵DF=BE
∴△BCE≌△DCF(SAS)
∴CE=CF
(2)GE=BE+GD成立
理由:∵∠BCD=90°∠GCE=45°
∴∠BCE+∠GCD=45°
∵△BCE≌△DCF(已证)
∴∠BCE=∠DCF
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=45°
 ∴∠ECG=∠FCG=45°
∴∠ECG=∠FCG=45°
∵CE=CF ,CG=CG
∴△ECG≌△FCG(SAS)
∴GE=FG
∵FG=GD+DF
∴GE=BE+GD
 (3)①
(3)①
解:过点C作CG⊥AD交AD的延长线于点G,
由(1)和题设知 DE=DG+BE.
设DG=x,则AD=12-x,DE=x+6,
在Rt△ADE中,AD2+AE2=DE2
∴ 62+(12-x)2=(x+6)2 解得 x=4.
∴DE=6+4=10.
② 15.


科目:初中数学 来源: 题型:
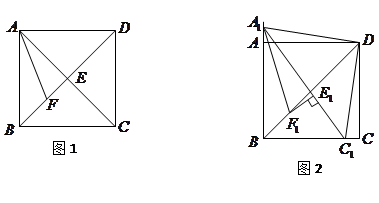
如图1,在正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)点![]() 从点
从点![]() 出发,沿着线段
出发,沿着线段![]() 向点
向点![]() 运动(不与点
运动(不与点![]() 重合),同时点
重合),同时点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的延长线运动,点
的延长线运动,点![]() 与
与![]() 的运动速度相同,当动点
的运动速度相同,当动点![]() 停止运动时,另一动点
停止运动时,另一动点![]() 也随之停止运动.如图2,
也随之停止运动.如图2,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,请猜想
,请猜想![]() ,
,![]() 与
与![]() 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当![]() ,
,![]() 时,求
时,求![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源:2012届山东省章丘市六中片区九年级学业水平考试数学卷 题型:解答题
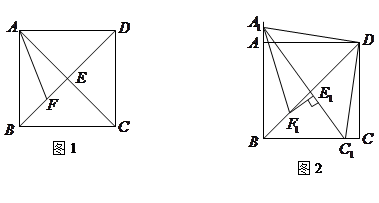
如图1,在正方形 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
,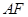 平分
平分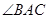 ,交
,交 于点
于点 .
.
(1)求证: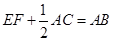 ;
;
(2)点 从点
从点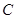 出发,沿着线段
出发,沿着线段 向点
向点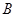 运动(不与点
运动(不与点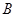 重合),同时点
重合),同时点 从点
从点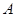 出发,沿着
出发,沿着 的延长线运动,点
的延长线运动,点 与
与 的运动速度相同,当动点
的运动速度相同,当动点 停止运动时,另一动点
停止运动时,另一动点 也随之停止运动.如图2,
也随之停止运动.如图2,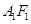 平分
平分 ,交
,交 于点
于点 ,过点
,过点 作
作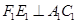 ,垂足为
,垂足为 ,请猜想
,请猜想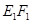 ,
,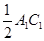 与
与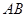 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当 ,
,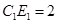 时,求
时,求 的长
的长
查看答案和解析>>
科目:初中数学 来源:2011—2012学年广东省江门市第三中学八年级下学期期末模拟考试数学试卷 题型:解答题
如图1,在正方形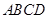 中,点
中,点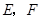 分别为边
分别为边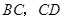 的中点,
的中点,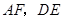 相交于点
相交于点 ,则可得结论:①
,则可得结论:①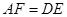 ;②
;②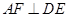 .(不需要证明)
.(不需要证明)
(1)如图2,若点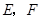 不是正方形
不是正方形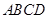 的边
的边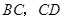 的中点,但满足
的中点,但满足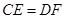 ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
(2)如图3,若点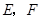 分别在正方形
分别在正方形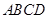 的边
的边 的延长线和
的延长线和 的延长线上,且
的延长线上,且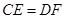 ,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
(3)如图4,在(2)的基础上,连接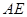 和
和 ,若点
,若点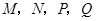 分别为
分别为 的中点,请判断四边形
的中点,请判断四边形 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.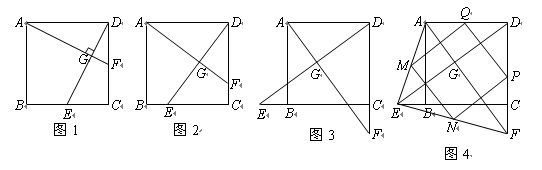
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省章丘市片区六中九年级学业水平考试数学卷(解析版) 题型:解答题
如图1,在正方形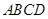 中,对角线
中,对角线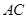 与
与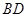 相交于点
相交于点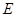 ,
,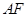 平分
平分 ,交
,交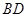 于点
于点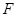 .
.
1.求证: ;
;
2.点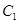 从点
从点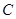 出发,沿着线段
出发,沿着线段 向点
向点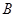 运动(不与点
运动(不与点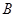 重合),同时点
重合),同时点 从点
从点 出发,沿着
出发,沿着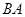 的延长线运动,点
的延长线运动,点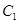 与
与 的运动速度相同,当动点
的运动速度相同,当动点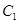 停止运动时,另一动点
停止运动时,另一动点 也随之停止运动.如图2,
也随之停止运动.如图2,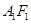 平分
平分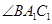 ,交
,交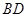 于点
于点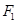 ,过点
,过点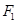 作
作 ,垂足为
,垂足为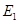 ,请猜想
,请猜想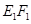 ,
,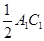 与
与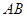 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
3.在(2)的条件下,当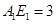 ,
, 时,求
时,求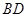 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省章丘市片区九年级学业水平考试数学卷 题型:解答题
如图1,在正方形 中,对角线
中,对角线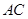 与
与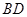 相交于点
相交于点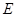 ,
, 平分
平分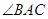 ,交
,交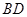 于点
于点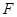 .
.
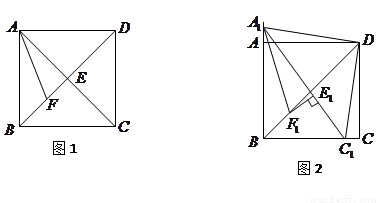
(1)求证: ;
;
(2)点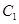 从点
从点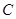 出发,沿着线段
出发,沿着线段 向点
向点 运动(不与点
运动(不与点 重合),同时点
重合),同时点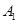 从点
从点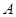 出发,沿着
出发,沿着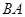 的延长线运动,点
的延长线运动,点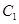 与
与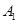 的运动速度相同,当动点
的运动速度相同,当动点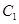 停止运动时,另一动点
停止运动时,另一动点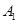 也随之停止运动.如图2,
也随之停止运动.如图2,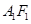 平分
平分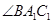 ,交
,交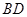 于点
于点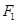 ,过点
,过点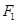 作
作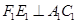 ,垂足为
,垂足为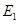 ,请猜想
,请猜想 ,
,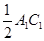 与
与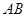 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当 ,
, 时,求
时,求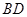 的长
的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com