
 图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米)
图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米) 分析 由“旋转的角度=速度×时间”来计算得到小明绕点O旋转了75度.如图,过点C作CE⊥OB于点E,构建矩形BDCE和直角△OEC,利用矩形的性质和解该直角三角形来求CD的长度即可.
解答 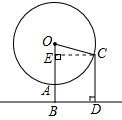 解:∵15×5°=75°,
解:∵15×5°=75°,
∴小明绕点O旋转了75度.
如图,过点C作CE⊥OB于点E,则四边形BDCE是矩形,
∴CD=BE.
由题意可知,∠AOC=75°,OC=40米,OB=45米.
在直角△OEC中,∵cos∠COE=$\frac{OE}{OC}$,
∴OE=OC•cos∠COE=40cos75°,
∴CD=EB=OB-OE=45-40cos75°≈34.6(米).
答:此时小明绕点O旋转了75度,他离地面的高度CD约为34.6米.
点评 本题考查了解直角三角形的应用.主要是余弦概念及运算,关键把实际问题转化为数学问题加以计算.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
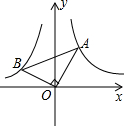 如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com