Question

⊙O的半径为5cm，弦AB∥CD，且AB=6cm，CD=8cm，则AB与CD之间的距离为

1. A.
   1cm
2. B.
   7cm
3. C.
   3cm或4cm
4. D.
   1cm或7cm

Answer 1

D
分析：先作出圆心与两弦的垂直距离，作图后很容易可以用勾股定理算出AB弦与圆心的距离为3cm，CD弦与圆心的距离为4cm，若AB、CD位于圆心异侧，则两平行弦的距离为3+4=7cm，AB、CD位于圆心同侧4-3=1cm．
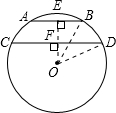
解答：解：过点O作OE⊥AB于E，交CD于F，
∵AB∥CD，
∴OF⊥CD，
∵OE过圆心，OE⊥AB，
∴EB=AB=3cm，
∵OB=5cm，
∴EO=4cm，
同理，OF=3cm，
∴EF=1cm，
当AB、CD位于圆心两旁时EF=7cm，
∴EF=1cm或EF=7cm．
故选D．
点评：本题结合勾股定理考查了垂径定理，解决与弦有关的问题，往往要作弦的弦心距，构造以弦心距、半径、弦长的一半为三边的直角三角形，利用勾股定理解答问题．