
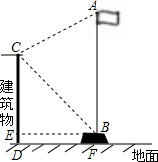
 如图,张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°,旗杆底部B点的俯角为45°,若旗杆底部B点到该建筑物的水平距离BE=9米,旗杆台阶的高BF=0.6米,A、B、F在同一直线上,求旗杆顶部A离地面的高度AF(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°,旗杆底部B点的俯角为45°,若旗杆底部B点到该建筑物的水平距离BE=9米,旗杆台阶的高BF=0.6米,A、B、F在同一直线上,求旗杆顶部A离地面的高度AF(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732). 科目:初中数学 来源: 题型:选择题
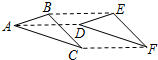 如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )
如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )| A. | BC∥EF | B. | AD=BE | C. | BE∥CF | D. | AC=EF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≠3 | B. | x≠3且x≠-3 | C. | x≠0且x≠-3 | D. | x≠-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数$y=\frac{1}{2}{(x-3)^2}-1$的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.
如图,二次函数$y=\frac{1}{2}{(x-3)^2}-1$的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com