
如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE,AE于点G、H试猜测线段AE和BD数量关系,并说明理由
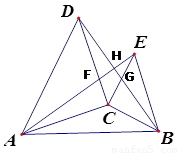
AE=BD,AE⊥BD
【解析】
试题分析:由于条件可知CD=AC,BC=CE,且可求得∠ACE=∠DCB,所以△ACE≌△DCB,即AE=BD,∠CAE=∠CDB;又因为对顶角相∠AFC=∠DFH,所以∠DHF=∠ACD=90°,即AE⊥BD
试题解析:猜测AE=BD,AE⊥BD;
理由如下:
∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB,
又∵△ACD和△BCE都是等腰直角三角形,
∴AC=CD,CE=CB,(4分)
∵在△ACE与△DCB中,
AC=DC
∠ACE=∠DCB
EC=BC
∴△ACE≌△DCB(SAS),
∴AE=BD,(6分)∠CAE=∠CDB;
∵∠AFC=∠DFH,∠FAC+∠AFC=90°,
∴∠DHF=∠ACD=90°,
∴AE⊥BD
故线段AE和BD的数量相等,位置是垂直关系
考点:1 全等三角形的判定;2 等腰直角三角形的性质


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
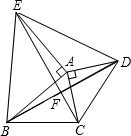 如图,△ACD和△AEB都是等腰直角三角形,∠EAB=∠CAD=90°,下列五个结论:①EC=BD;②EC⊥BD;③S四边形EBCD=
如图,△ACD和△AEB都是等腰直角三角形,∠EAB=∠CAD=90°,下列五个结论:①EC=BD;②EC⊥BD;③S四边形EBCD=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.
23、如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
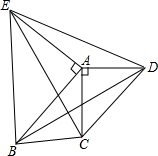 如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°.四边形ABCD是平行四边形,下列结论中错误的有( )
如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°.四边形ABCD是平行四边形,下列结论中错误的有( )查看答案和解析>>
科目:初中数学 来源: 题型:
 31、如图,△ACD和△ABE都是直角等腰三角形,∠DAC和∠EAB是直角,连接CE.
31、如图,△ACD和△ABE都是直角等腰三角形,∠DAC和∠EAB是直角,连接CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com