
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )

A.当x=3时,EC<EM B.当y=9时,EC>EM
C.当x增大时,EC•CF的值增大 D.当y增大时,BE•DF的值不变
D.
【解析】
试题分析:由图象可知,反比例函数图象经过(3,3),应用待定系数法可得该反比例函数关系式为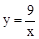 ,因此,
,因此,
当x=3时,y=3,点C与点M重合,即EC=EM,选项A错误;
根据等腰直角三角形的性质,当x=3时,y=3,点C与点M重合时,EM=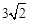 ,
当y=9时,
,
当y=9时,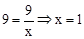 ,即EC=
,即EC=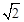 ,所以,EC<EM,选项B错误;
,所以,EC<EM,选项B错误;
根据等腰直角三角形的性质,EC=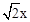 ,CF=
,CF=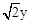 ,
即EC·CF=
,
即EC·CF=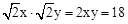 ,为定值,所以不论x如何变化,EC·CF的值不变,选项C错误;
,为定值,所以不论x如何变化,EC·CF的值不变,选项C错误;
根据等腰直角三角形的性质,BE=x,DF=y,所以BE·DF=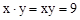 ,为定值,所以不论y如何变化,BE·DF的值不变,选项D正确.
,为定值,所以不论y如何变化,BE·DF的值不变,选项D正确.
故选D.
考点:1.反比例函数的图象和性质;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.等腰直角三角形的性质;5.勾股定理.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
 (2013•安徽)图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )
(2013•安徽)图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )查看答案和解析>>
科目:初中数学 来源:2013年安徽省中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(安徽卷)数学(解析版) 题型:选择题
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是

A.当x=3时,EC<EM B.当y=9时,EC>EM
C.当x增大时,EC·CF的值增大。 D.当y增大时,BE·DF的值不变。
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(安徽卷)数学(带解析) 题型:单选题
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是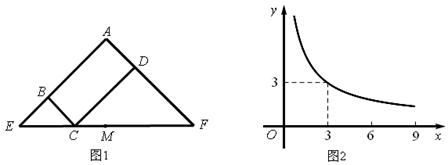
| A.当x=3时,EC<EM | B.当y=9时,EC>EM |
| C.当x增大时,EC·CF的值增大。 | D.当y增大时,BE·DF的值不变。 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com