
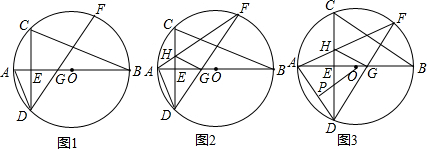
分析 (1)证明:连接BD.由∠AGD=∠DBG+∠BDG,∠ADG=∠ADE+∠EDG,可知只要证明∠CDF=∠BDF,∠ADC=∠DBA即可.
(2)欲证明CH=HG,只要证明△ACH≌△GAH即可.
(3)连接FO,过点F作FK⊥BG于点K,连接FB、AC,连接CG交AF于点R.由△OAP≌△FOK,推出FK=OP,FG=FB,FK=2GK,由DE∥FK,
推出∠GFK=∠CDG,由EG垂直平分CD,推出CG=DG=4,∠GCE=∠GDC,∠GCE=∠GFK,由AC=AG,∠CAH=∠GAH,推出CR=RG=2,tan∠HCR=tan∠GFK,推出$\frac{HR}{CR}$=$\frac{GK}{FK}$,即$\frac{HR}{2}$=$\frac{1}{2}$,求得HR=1,在Rt△HCR中,CH2=HR2+CR2=12+22=5,由此即可解决问题.
解答 (1)证明:连接BD.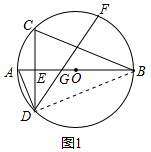
∵F为$\widehat{BC}$的中点,
∴∠CDF=∠BDF,
∵AB为⊙O的直径,CD⊥AB,
∴$\widehat{AC}$=$\widehat{AD}$,
∴∠ADC=∠DBA,
∴∠AGD=∠DBG+∠BDG,
∵∠ADG=∠ADE+∠EDG,
∴∠AGD=∠ADG.
(2)证明:连接AC.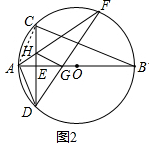
∵$\widehat{AC}$=$\widehat{AD}$,
∴AC=AD,
∵∠AGD=∠ADG,
∴AG=AD,
∴AC=AG,
∵F为$\widehat{BC}$的中点,
∴∠CAH=∠GAH,
在△AHC和△AHG中,
$\left\{\begin{array}{l}{AC=AG}\\{∠CAH=∠GAH}\\{AH=AH}\end{array}\right.$,
∴△ACH≌△GAH,
∴CH=HG.
(3)解:连接FO,过点F作FK⊥BG于点K,连接FB、AC,连接CG交AF于点R.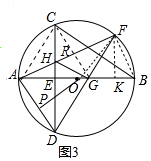
∵$\widehat{AC}$=$\widehat{AD}$,
∴AC=AD,
∵AE⊥CD,
∴∠DAE=∠CAE=2∠HAE,
∵∠FOB=2∠HAE
∴∠DAE=∠FOB,
∵OA=OF,∠OPA=∠FKO=90°,
∴△OAP≌△FOK,
∴FK=OP,
∵∠FBA=∠ADF,又∵∠AGD=∠ADG,∠AGD=∠FGB
∴∠FBG=∠FGB,
∴FG=FB,
∵FK⊥BG,
∴GK=KB,
∵OP=FK=GB,
∴FK=2GK
∵∠DEG=∠FKG=90°,
∴DE∥FK,
∴∠GFK=∠CDG,
∵EG垂直平分CD,
∴CG=DG=4,
∴∠GCE=∠GDC,
∴∠GCE=∠GFK,
∵AC=AG,∠CAH=∠GAH,
∴CR=RG=2,
∵∠HCR=∠GFK,
∴tan∠HCR=tan∠GFK,
∴$\frac{HR}{CR}$=$\frac{GK}{FK}$,即$\frac{HR}{2}$=$\frac{1}{2}$,
∴HR=1,
在Rt△HCR中,CH2=HR2+CR2=12+22=5,
∴CH=$\sqrt{5}$,
∴HG=CH=$\sqrt{5}$.
点评 本题考查圆综合题、锐角三角函数、垂径定理、圆周角定理、勾股定理、线段的垂直平分线的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线,正确寻找中全等三角形,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 在只装了红球的袋子中摸到白球 | |
| B. | 某射击运动员射击一次,命中靶心 | |
| C. | 任意画一个三角形,其内角和是180° | |
| D. | 掷一枚质地均匀的正方体骰子,向上的一面点数是3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=mx+n与双曲线y=$\frac{k}{x}$相交于A(-1,2)、B(2,b)两点,与y轴相交于点C.
如图,直线y=mx+n与双曲线y=$\frac{k}{x}$相交于A(-1,2)、B(2,b)两点,与y轴相交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com