
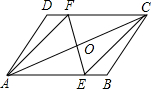
 已知如图,O为平行四边形ABCD的对角线AC的中点,EF经过点O,且与AB交于E,与CD 交于F.
已知如图,O为平行四边形ABCD的对角线AC的中点,EF经过点O,且与AB交于E,与CD 交于F. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知抛物线y=ax2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论:
已知抛物线y=ax2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论:查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(辽宁丹东) 题型:填空题
.
从边长为a的大正方形纸板中间挖去一个边长为b的小正方形后,将其截成四个相同的等腰梯形﹙如图①﹚,可以拼成一个平行四边形﹙如图②﹚.
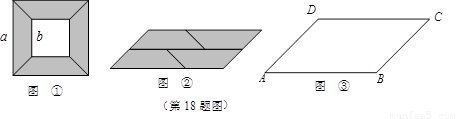
现有一平行四边形纸片ABCD﹙如图③﹚,已知∠A=45°,AB=6,AD=4.若将该纸片按图②方式截成四个相同的等腰梯形,然后按图①方式拼图,则得到的大正方形的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com