

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(09)(解析版) 题型:解答题
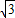 ),B(
),B( ,
,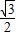 ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,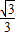 ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
查看答案和解析>>
科目:初中数学 来源:2009年内蒙古赤峰市中考数学试卷(解析版) 题型:解答题
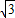 ),B(
),B(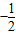 ,
,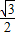 ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,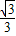 ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
查看答案和解析>>
科目:初中数学 来源:2009年内蒙古赤峰市中考数学试卷(解析版) 题型:填空题
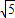 ,0)沿y轴正方向平移1个单位长度得到点P,连接PO,再将PO绕点O按顺时针方向旋转120°,则PO在旋转过程中扫过的扇形面积为 .(结果保留π)
,0)沿y轴正方向平移1个单位长度得到点P,连接PO,再将PO绕点O按顺时针方向旋转120°,则PO在旋转过程中扫过的扇形面积为 .(结果保留π)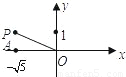
查看答案和解析>>
科目:初中数学 来源:2005年重庆市课改实验区初中学业考试数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com