
���� ��1���������������ȷ��Ŀ�еĴ���ʽ��ʾ�ĺ��壬������Խ����
��2��������������г���Ӧ��һԪ���η��̣��Ӷ����Խ���⣬ע��x��15��
��� �⣺��1��������ɵã�
����ʽ��60-50+x����ʾ���Ǻ�ÿ������Ʒ������
����ʽ��400-10x����ʾ���Ǻ�ÿ�����������
�ʴ�Ϊ�����Ǻ�ÿ������Ʒ���������Ǻ�ÿ�����������
��2�������⣬�ɵã�
��60-50+x����400-10x��=6000��
��ã�x1=10��x2=20��
��20��15��
��x=20���������⣬
��x=10��
��Ӧ�Ǽ�10Ԫ��
���� ���⿼��һԪ���η��̵�Ӧ�ã�����Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ���������г���Ӧ�ķ��̣�ע�ⷽ�̽����Ϻ����Ҫ����


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
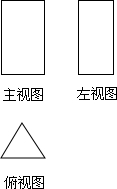 ��1����ͼ��ʾΪһ�����������ͼ��
��1����ͼ��ʾΪһ�����������ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x+y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x+2y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}{\frac{1}{2}x+y=50}\\{x+\frac{2}{3}y=50}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x+\frac{1}{2}y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 75�� | B�� | 60�� | C�� | 45�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
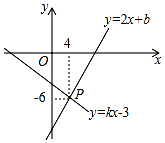 ��ͼ����֪һ�κ���y=2x+b��y=kx-3��k��0����ͼ���ڵ�P�����Ԫһ�η�����$\left\{\begin{array}{l}2x-y=-b\\ kx-y=3\end{array}\right.$�Ľ���$\left\{\begin{array}{l}{x=4}\\{y=-6}\end{array}\right.$��
��ͼ����֪һ�κ���y=2x+b��y=kx-3��k��0����ͼ���ڵ�P�����Ԫһ�η�����$\left\{\begin{array}{l}2x-y=-b\\ kx-y=3\end{array}\right.$�Ľ���$\left\{\begin{array}{l}{x=4}\\{y=-6}\end{array}\right.$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
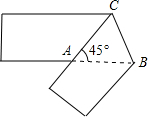 ��ͼ������Ϊ1cm�ij�����ֽ����BC�۵���ʹ��CAB=45�㣬���۵����ص����ֵ����Ϊ��������
��ͼ������Ϊ1cm�ij�����ֽ����BC�۵���ʹ��CAB=45�㣬���۵����ص����ֵ����Ϊ��������| A�� | $\frac{\sqrt{3}}{2}$ cm2 | B�� | $\sqrt{3}$ cm2 | C�� | $\sqrt{2}$ cm2 | D�� | $\frac{\sqrt{2}}{2}$ cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ƽ��ֱ������ϵxOy�У�������y=mx2-2mx+m-2��m��0���Ķ���ΪA����x�ύ��B��C���㣨��B�ڵ�C��ࣩ����y�Ḻ���ύ�ڵ�D��
��ƽ��ֱ������ϵxOy�У�������y=mx2-2mx+m-2��m��0���Ķ���ΪA����x�ύ��B��C���㣨��B�ڵ�C��ࣩ����y�Ḻ���ύ�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
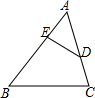 ��ͼ����ADE=��B����AD��AB=2��3�����ADE���ABC�������Ϊ4��9��
��ͼ����ADE=��B����AD��AB=2��3�����ADE���ABC�������Ϊ4��9���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com